Valutazione delle performance di un modello di classificazione binaria

La fase di valutazione del modello inizia quando creiamo un set di validazione che consiste in esempi che l'algoritmo di apprendimento non ha visto durante l'addestramento. Se il nostro modello si comporta bene su questo set allora possiamo dire che generalizza bene ed è di buona qualità.

Il modo più comune per valutare se un modello è valido o meno è calcolare una metrica di performance proprio sul set di validazione o di test.

Questo articolo si concentrerà sulle metriche di performance per i modelli di classificazione. Vale la pena specificarlo perché task di regressione hanno metriche tracciabili completamente diverse. Qui un articolo sulle metriche di valutazione di un modello di regressione.

Metriche di performance per la classificazione

Le metriche che andremo a coprire sono:

• Accuratezza
• Precisione e richiamo
• Punteggio F1
• Log loss
• ROC-AUC
• Coefficiente di correlazione di Matthews (MCC)

Accuratezza

Quando vogliamo analizzare la performance di un classificatore binario, la metrica più comune e accessibile è sicuramente la accuratezza (in inglese accuracy). Essa non fa altro che indicarci quante volte il nostro modello ha correttamente classificato un item nel nostro dataset rispetto al totale.

Infatti la formula per l'accuratezza è la divisione tra numero di risposte corrette e il totale delle risposte

\[ accuratezza = \frac{numero\_risposte\_corrette}{numero\_risposte\_totali} \]

La accuratezza tiene conto delle performance del modello in senso stretto. Vale a dire che non ci permette di comprendere il contesto nel quale stiamo operando.

Presa fuori dal contesto, la accuratezza è una metrica molto delicata da interpretare.

Ad esempio, è sconsigliato usare la accuratezza come metrica di valutazione quando operiamo con un dataset sbilanciato, dove le classi sono distribuite in maniera impari. Se la accuratezza non è altro che il rapporto tra risposte corrette sul totale, allora capirete che se una classe compone il 90% del nostro dataset e il nostro modello (erroneamente) classifica ogni esempio nel dataset con quella classe specifica, allora la sua accuratezza sarà del 90%.

Se non siamo attenti potremmo pensare che il nostro modello sia molto performante, quando in realtà è molto lontano dall'esserlo.

La accuratezza è però una metrica sensata da usare se siamo sicuri che il nostro dataset sia bilanciato e che i dati siano di alta qualità.

Precisione e richiamo

Per comprendere al meglio i concetti di precisione e richiamo useremo una matrice di confusione (confusion matrix) per introdurre l'argomento. Si chiama così proprio perché comunica all'analista il grado di errore (e quindi di confusione) del modello.

Per creare una confusion matrix non dobbiamo far altro che elencare le classi effettive presenti nel dataset su righe e e quelle che il modello deve prevedere nelle colonne. Il valore delle celle corrisponde alla risposta del modello sotto quelle condizioni.

Vediamo un esempio usando Sklearn come fonte

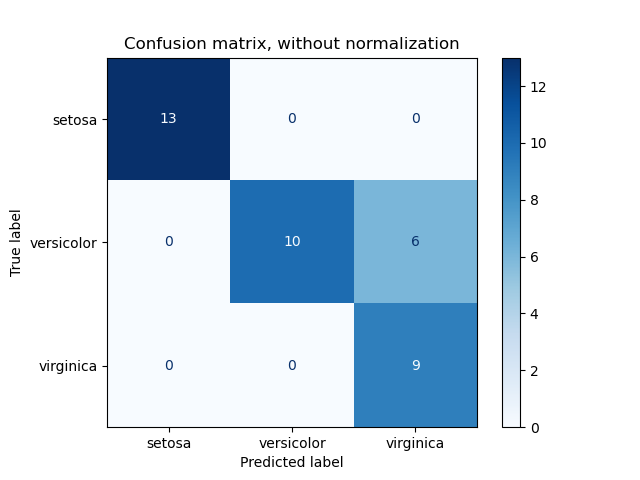
Questo è un esempio di una matrice di confusione per un classificatore binario applicato al famoso Iris dataset.

I valori sulla diagonale indicano i punti in cui la predizione del modello di classificazione corrisponde alla classe reale presente nel dataset. Più elementi sono presenti sulla diagonale, più le nostre predizioni sono corrette (attenzione, non ho detto che il modello sia performante! Ricordiamoci il discorso della accuratezza di prima).

Andiamo a rappresentare in maniera astratta la matrice di confusione in modo da comprendere al meglio i valori che riempiono le celle.

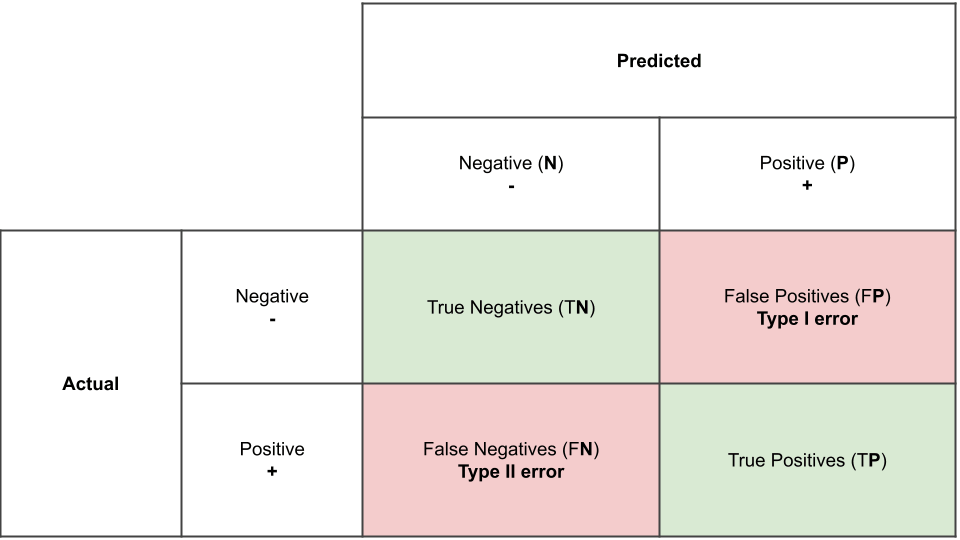
Vediamo una serie di etichette: true negatives (veri negativi), true positives (veri positivi), false negatives (falsi negativi) e false positives (falsi positivi). Vediamone uno ad uno.

• Veri negativi (TN): contiene gli esempi che sono stati correttamente classificati come negativi.
• Veri positivi (TP): contiene gli esempi che sono stati correttamente classificati come positivi.
• Falsi negativi (FN): contiene gli esempi che sono stati erroneamente classificati come negativi e che quindi sono in realtà positivi
• Falsi positivi (FP): contiene gli esempi che sono stati erroneamente classificati come positivi e che quindi sono in realtà negativi

Usando una matrice di confusione riusciamo quindi a capire meglio il comportamento del nostro classificatore e come migliorarlo ulteriormente.

Per continuare, vediamo come trarre la formula della accuratezza dalla matrice di confusione

\[ accuratezza = \frac{TN + TP}{TN + TP + FP + FN} \]

Questa non è altro che il numero di risposte corrette diviso il totale.

Definiamo ora la precisione con la formula

\[ precisione = \frac{TP}{TP + FP} \]

Come si interpreta? La precisione non è altro che la accuratezza calcolata solo classi positive. Essa è anche chiamata specificità poiché definisce quanto sensibile è uno strumento quando c'è il segnale da riconoscere. Di fatto, la metrica ci informa quanto spesso siamo corretti quando classifichiamo una classe come positiva.

Facciamo un'altro esempio: abbiamo installato un sistema di allarme in casa con un algoritmo di riconoscimento facciale. Questo è collegato a delle telecamere e ad una centralina che invia una notifica su una app sul nostro cellulare se in casa entra qualcuno che non riconosce come amico o familiare.

Un modello con alta precisione ci allerterà poche volte, ma quelle volte che lo farà possiamo essere abbastanza sicuri che si tratti veramente di un intruso! Quindi, il modello è abile a distinguere correttamente un intruso da un familiare quando in casa c'è effettivamente un intruso.

Il richiamo invece rappresenta l'altro ago della bilancia. Se siamo interessati a riconoscere quanti più classi positive possibili, allora il nostro modello dovrà avere un richiamo alto.

La sua formula è

\[ richiamo = \frac{TP}{TP + FN} \]

In pratica significa che qui dobbiamo tener conto dei falsi negativi invece dei falsi positivi. Il richiamo viene anche chiamato sensibilità perché all'aumentare del richiamo, il nostro modello diventa sempre meno preciso e classifica anche classi negative come positive.

Osserviamo un esempio che include il richiamo: siamo dei radiologi e abbiamo addestrato un modello che usa la computer vision per classificare la presenza di eventuali tumori ai polmoni. In questo caso vogliamo che il nostro modello abbia alto richiamo, in quanto vogliamo essere sicuri che ogni minimo esempio considerato positivo da parte del modello venga sottoposto a ispezione umana. Non vogliamo che un tumore maligno passi inosservato, e accetteremo volentieri dei falsi positivi.

Per riassumere, vediamo questa analogia

Un modello ad alta precisione è conservativo: non riconosce sempre la classe correttamente, ma quando lo fa, possiamo stare molto tranquilli che la sua risposta sia corretta.

Un modello ad alta precisione è liberale: riconosce una classe molto più spesso, ma nel farlo tende a includere anche molto rumore (falsi positivi).

Il lettore attento e curioso avrà dedotto che è impossibile avere un modello con alta precisione e alto richiamo. Infatti, queste due metriche sono complementari: se aumentiamo una, l'altra deve diminuire. Si tratta del precision/recall trade-off.

Il nostro obiettivo da analisti è quello di contestualizzare e capire quale metrica ci offre più valore.

Punteggio F1

A questo punto è chiaro che usare precisione o richiamo come metrica di valutazione è difficile perché possiamo solo usarne una a scapito dell'altra. Il punteggio F1 risolve proprio questo problema.

Infatti, il punteggio F1 combina precisione e richiamo in una sola metrica.

\[ F1 = 2 \times \frac{precisione \times richiamo}{precisione + richiamo} \]

Questa è la media armonica di precisione e richiamo, ed è probabilmente la metrica più usata per valutare modelli di classificazione binaria.

Se il nostro punteggio F1 aumenta, vuol dire che il nostro modello ha aumentato le performance per precisione, richiamo o per entrambi.

Log loss

La log loss è una metrica di valutazione comune, soprattutto su Kaggle. Conosciuta anche come cross-entropia o entropia incrociata nel contesto del deep learning, questa misura la differenza tra le probabilità delle previsioni del modello e le probabilità della realtà osservata. L'obiettivo di questa metrica è di stimare la probabilità che un esempio abbia una classe positiva.

Questa metrica è matematicamente più complessa delle precedenti e non c'è bisogno di andare in profondità per intuire la sua utilità nel valutare un sistema di classificazione binario.

Ecco la formula per completezza

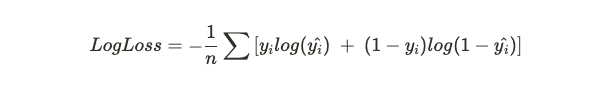
\( n \) sta per il numero di esempi nel dataset, \( y_i \) sta per la realtà osservata e \( y\hat{}_i \) sta per la predizione del modello.

Non continuerò con la spiegazione di questa formula perché andrei fuori traccia. Google è il vostro migliore amico 🙂

ROC-AUC

La metrica ROC-AUC si basa su una rappresentazione grafica della curva ROC (receiving operating characteristic curve). Non proverò a spiegarla a parole mie, perché stavolta Wikipedia fa veramente un ottimo lavoro

le curve ROC […] sono degli schemi grafici per un classificatore binario. Lungo i due assi si possono rappresentare la sensibilità e (1-specificità), rispettivamente rappresentati da True Positive Rate (TPR, frazione di veri positivi) e False Positive Rate (FPR, frazione di falsi positivi). In altre parole, si studiano i rapporti fra allarmi veri (hit rate) e falsi allarmi.

La frase finale in grassetto (applicato da me) è quella che rende intuitiva la descrizione della curva ROC che abbiamo appena letto. Ovviamente vogliamo che il rapporto tra allarmi veri e falsi sia in favore di quelli veri, perché modelli più performanti faranno esattamente questo.

Vediamo come si presenta tale grafico

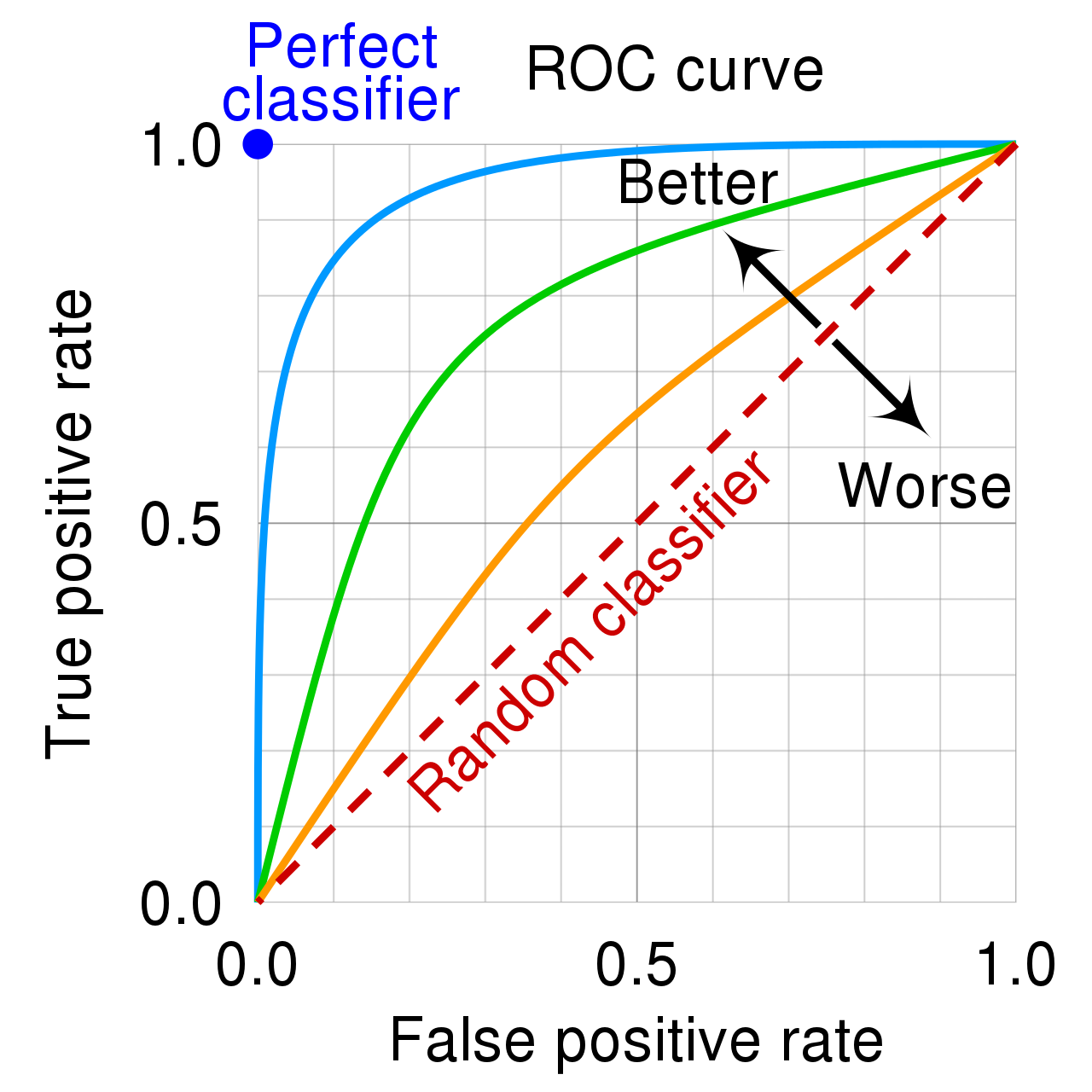
AUC sta per Area Under the Curve (area al di sotto della curva). Se poniamo l'attenzione sulla linea blu, vediamo che al di sotto di essa c'è di fatto una area più grande rispetto alle linee verde arancione. La linea tratteggiata indica un metrica di ROC-AUC del 50%.

Di conseguenza un buon modello avrà una ROC-AUC grande, mentre un modello scarso si posizionerà vicino alla linea tratteggiata, che non è altro che un modello che risponde in maniera casuale.

La metrica ROC-AUC è anche molto utile per confrontare diversi modelli uno contro l'altro.

Coefficiente di correlazione di Matthews (MCC)

Vediamo qui l'ultima metrica di valutazione per un modello di classificazione binaria che è concepito per valutare correttamente anche modelli addestrati su dataset non bilanciati.

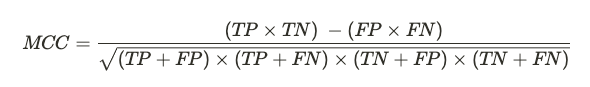
Sembra uno scioglilingua, ma in realtà questa formula si comporta come un coefficiente di correlazione. Essa va quindi da +1 a -1. Un valore che tende a +1 misura la qualità delle predizioni del nostro classificatore anche in contesti con classi sbilanciate nel dataset, poiché indica una correlazione tra valori reali osservati e previsioni fatte dal nostro modello.

Conclusione

Come per le metriche valutazione dei modelli di regressione, Sklearn mette a disposizione parecchi metodi per calcolare rapidamente queste metriche. Qui un link alla documentazione.

Come nota finale, queste sono metriche per la valutazione di un classificatore binario. Per la classificazione multi-classe, ad esempio, basta applicare una di queste metriche ad ogni classe e poi applicare una strategia che vada a generalizzare su tutti gli esempi, come la media (micro/macro averaging). Ma questo è un discorso per un altro articolo :)