Tabella dei Contenuti
Il feature engineering è un passaggio essenziale in una pipeline di machine learning, in cui i dati grezzi vengono trasformati in caratteristiche più significative che aiutano il modello a comprendere meglio le relazioni tra i dati.
Feature engineering significa spesso applicare delle trasformazioni ai dati a disposizione per sovrascrivere o crearne dei nuovi che, nel contesto del machine learning e data science, vengono usati per addestrare un modello che può performance meglio grazie proprio a queste trasformazioni.
In questo articolo, esploreremo tecniche avanzate di feature engineering per la gestione di valori numerici con la libreria Scikit-Learn di Python, Numpy e altre per rendere i tuoi modelli di machine learning ancora più efficaci.
- Una solida lista di tecniche di feature engineering per dati numerici provenienti dalla suite Scikit-Learn, Numpy e Scipy per migliorare le prestazioni dei modelli di machine learning
- Implementazione pratica di trasformazioni logaritmiche e Box-Cox per normalizzare distribuzioni e linearizzare relazioni nei dati
- Casi d'uso specifici per ciascuna tecnica e come queste possono rivelare pattern latenti, affinare la rappresentazione delle variabili e migliorare l'interpretabilità dei modelli
Questo articolo è legato alla Guida alla gestione delle variabili categoriali, che mostra come fare feature engineering per le variabili non numeriche.
Casi d'uso
L'ottimizzazione delle feature è un elemento chiave nel miglioramento della qualità dei modelli di machine learning, soprattutto nell'analisi di dataset complessi. L'applicazione mirata di tecniche di feature engineering offre diversi vantaggi:
- Rivelazione di pattern latenti nei dati: Questa tecnica permette di scoprire relazioni nascoste e strutture non evidenti a prima vista.
- Affinamento della rappresentazione delle variabili: Il processo trasforma i dati grezzi in formati più adatti all'apprendimento automatico.
- Gestione delle sfide legate alla distribuzione e alla natura intrinseca dei dati: Questo approccio affronta problemi come skewness, outlier e scalabilità delle variabili.
L'implementazione precisa di queste tecniche di ottimizzazione delle feature porta a un potenziamento significativo delle prestazioni dei modelli di machine learning.
Questi miglioramenti si riflettono in vari aspetti del funzionamento dei modelli, dalla loro capacità predittiva alla loro interpretabilità. La qualità superiore delle feature utilizzate permette ai modelli di cogliere sfumature e pattern complessi nei dati, che altrimenti potrebbero rimanere nascosti.
Inoltre, l'ottimizzazione delle feature contribuisce a rendere i modelli più robusti e generalizzabili, caratteristiche essenziali per applicazioni nel mondo reale e riducendo la possibilità di overfitting.
Partiamo con alcune tecniche di feature engineering utili.
Normalizzazione
Probabilmente la prima tecnica di feature engineering numerico che un data scientist impara - la normalizzazione (anche nota come scaling) è un metodo in cui modifichiamo una variabile sottraendo la media e dividendola per la deviazione standard.
\[ X_{\text{scaled}} = \frac{X - \text{mean}(X)}{\text{std}(X)} \]
Eseguire questa trasformazione significa che la variabile risultante avrà una media di 0 e una deviazione standard e una varianza di 1.
Nel machine learning, soprattutto nel deep learning, avere variabili confinate tra valori specifici (ad esempio proprio 0 e 1) aiuta il modello a convergere prima ad una soluzione ottimale.
Questa tecnica è una trasformazione appresa - quindi utilizziamo i dati di training per ricavare i valori corretti di e e poi questi valori vengono utilizzati per eseguire le trasformazioni quando vengono applicate a nuovi dati.
Va notato che questa trasformazione non modifica la distribuzione, ma ridimensiona i valori.
Applicazione pratica
Useremo il famoso wine dataset di Sklearn per un task di classificazione. Confronteremo le performance usando e non usando la normalizzazione in matrici di confusione, usando Sklearn.
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import confusion_matrix
import numpy as np
X, y = load_wine(return_X_y=True)
# Dividi i dati in set di training e test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30, random_state=42)
# Funzione per addestrare il modello e ottenere la matrice di confusione
def get_confusion_matrix(X_train, X_test, y_train, y_test):
model = KNeighborsClassifier(n_neighbors=5)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
return confusion_matrix(y_test, y_pred)
# Ottieni la matrice di confusione senza normalizzazione
cm_without_norm = get_confusion_matrix(X_train, X_test, y_train, y_test)
# Normalizza i dati
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
# Ottieni la matrice di confusione con normalizzazione
cm_with_norm = get_confusion_matrix(X_train_scaled, X_test_scaled, y_train, y_test)
# Crea la figura con due subplot affiancati
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(20, 8))
# Funzione per creare l'heatmap
def plot_heatmap(ax, cm, title):
sns.heatmap(cm, annot=True, fmt='d', cmap='viridis', ax=ax, cbar=False)
ax.set_title(title, fontsize=16, pad=20)
ax.set_xlabel('Predetto', fontsize=12, labelpad=10)
ax.set_ylabel('Reale', fontsize=12, labelpad=10)
# Plotta le heatmap
plot_heatmap(ax1, cm_without_norm, 'Matrice di Confusione\nSenza Normalizzazione')
plot_heatmap(ax2, cm_with_norm, 'Matrice di Confusione\nCon Normalizzazione')
# Aggiungi una colorbar comune
cbar_ax = fig.add_axes([0.92, 0.15, 0.02, 0.7])
sm = plt.cm.ScalarMappable(cmap='viridis', norm=plt.Normalize(vmin=0, vmax=np.max([cm_without_norm, cm_with_norm])))
fig.colorbar(sm, cax=cbar_ax)
# Aggiusta il layout e mostra il grafico
plt.tight_layout(rect=[0, 0, 0.9, 1])
plt.show()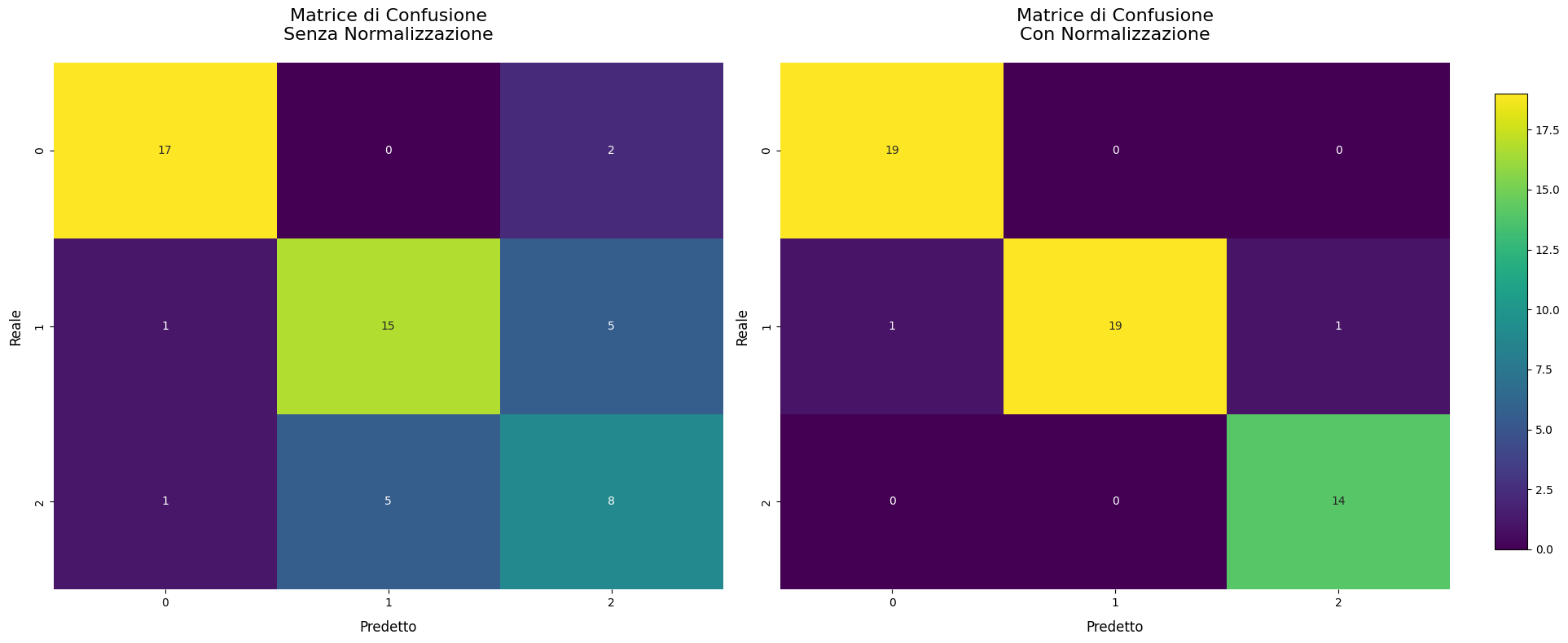
Il delta di miglioramento è del circa 30% - la normalizzazione su alcuni algoritmi ha un impatto talmente grande che non applicarla adeguatamente rappresenta un errore grave da parte del data scientist.
RobustScaler e MinMaxScaler.Dagli esempi di Sklearn è disponibile un grafico più complesso che mostra i bordi di classificazione del modello KNNClassifier
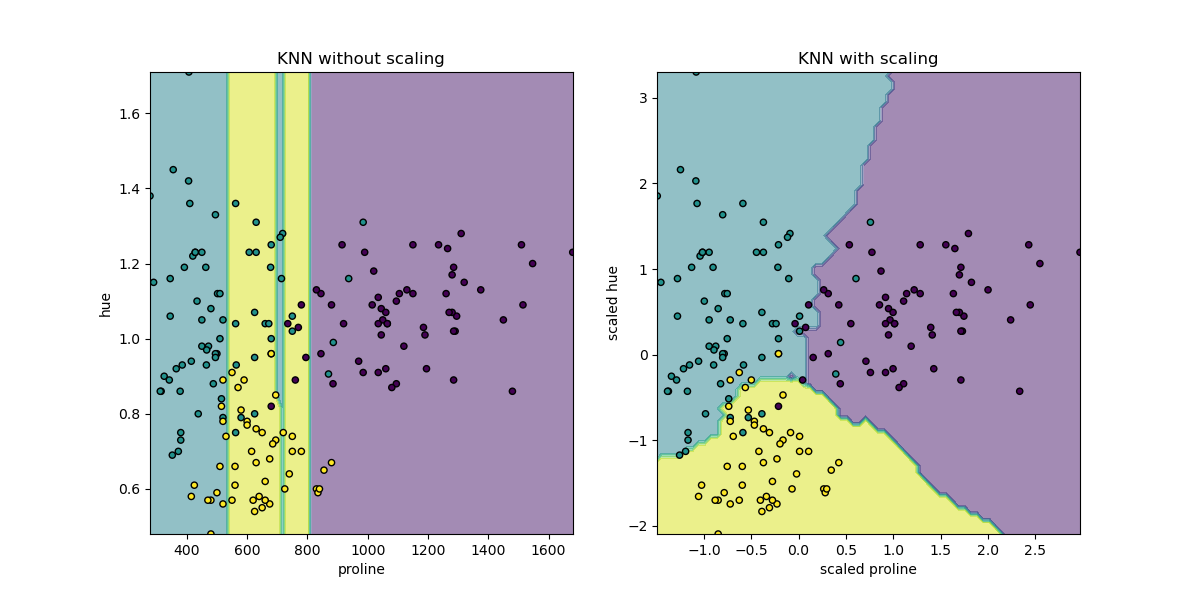
Feature polinomiali
Le feature polinomiali sono utili per introdurre non linearità nei modelli lineari. La classe PolynomialFeatures di Scikit-Learn permette di generare sia caratteristiche polinomiali che termini di interazione tra le variabili.

Data una feature originale \( x \), le feature polinomiali possono includere:
- \( x^2 \) (quadratica)
- \( x^3 \) (cubica)
- \( x^4 \) (quarta potenza)
- e così via
Per modelli con multiple feature \( (x_1, x_2,...,x_n) \), si possono creare anche termini di interazione:
- \( x_1 \times x_2 \)
- \( x^2_1 \times x_2 \)
- \( x_1 \times x^2_2 \)
e così via.
Lo scopo principale è permettere a modelli lineari di apprendere relazioni non lineari nei dati senza modificare l'algoritmo di base.
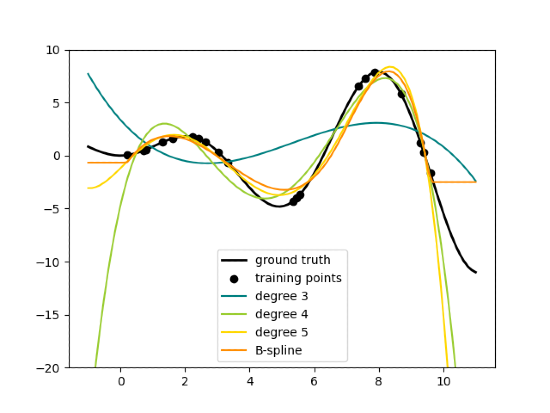
Il loro principale punto di forza risiede nell'aumentare notevolmente la flessibilità del modello, permettendo anche a modelli lineari di catturare relazioni non lineari nei dati. Questo si traduce in:
- Capacità di modellare curve e superfici complesse nello spazio delle feature
- Potenziale contributo positivo delle prestazioni su dati intrinsecamente non lineari
- Il modello, pur catturando relazioni non lineari, mantiene una struttura di base lineare. Ciò permette di usare strumenti di analisi familiari e interpretare i coefficienti più facilmente rispetto a modelli non lineari complessi, anche se questa semplicità diminuisce con l'aumento del grado polinomiale.
Un altro vantaggio cruciale è la capacità di rivelare interazioni nascoste tra variabili. In domini come la fisica o l'economia, dove le relazioni sono spesso non lineari, questa caratteristica si rivela particolarmente preziosa.
Per quanto riguarda gli svantaggi invece
- Aumenta rapidamente la dimensionalità del dataset, creando colonne aggiuntive per ogni feature sottoposte all'algoritmo
- Può portare a overfitting se usato in modo eccessivo
- Richiede più risorse computazionali, proprio a causa della necessità di elaborare un numero maggiori di feature
Dal punto di vista pratico, l'implementazione delle feature polinomiali è relativamente semplice grazie ad Sklearn in Python. Vedremo a breve come fare.
Applicazione Pratica
PolynomialFeatures è una classe di Scikit-learn utilizzata per generare feature polinomiali. Si trova nel modulo sklearn.preprocessing.
L'oggetto trasforma un array di input di grado 1 in un nuovo array contenente tutti i termini polinomiali fino a uno specifico grado. Ad esempio, se le feature originali sono \( [a,b] \), con grado=2 si ottengono le feature \( [1, a,b,a^2, ab, b^2] \).
Gli argomenti dell'oggetto sono i seguenti
degree(int, default=2):- Il grado del polinomio
- Determina il massimo grado dei termini polinomiali generati
interaction_only(bool, default=False):- Se True, genera solo termini di interazione
- Non produce potenze di singole feature
include_bias(bool, default=True):- Se True, include una colonna di 1 (il termine di bias)
- Utile quando si usa il risultato con modelli che non hanno un termine di intercetta separato
order('C' o 'F', default='C'):- Determina l'ordine di output delle feature
- 'C' per ordine C-style (ultime feature cambiano più velocemente), 'F' per ordine Fortran-style
Ecco un esempio di come implementare l'oggetto in Sklearn.
from sklearn.preprocessing import PolynomialFeatures
import numpy as np
X = np.array([[1, 2], [3, 4]])
poly = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly.fit_transform(X)
print(X_poly)
# Output: [[1. 2. 1. 2. 4.]
# [3. 4. 9. 12. 16.]]
print(poly.get_feature_names(['x1', 'x2']))
# Output: ['x1', 'x2', 'x1^2', 'x1 x2', 'x2^2']Ora queste feature possono informare un modello di machine learning e possibilmente aiutarlo a performare meglio.
FunctionTransformer
FunctionTransformer è uno strumento versatile in Scikit-learn che permette di incorporare funzioni personalizzate nel processo di trasformazione dei dati. Esso consente di applicare una funzione arbitraria ai dati come parte di una pipeline di preprocessing o feature engineering. Essenzialmente, trasforma una funzione Python in un oggetto "transformer" (non come il modello di deep learning, ma quello di Sklearn) compatibile con l'API di Scikit-learn.

FunctionTransformer prende una funzione Python come input principale e crea un oggetto transformer che, quando applicato ai dati, esegue quella funzione. Può anche essere utilizzato in combinazione con altri transformer o all'interno di una pipeline Scikit-learn.
Un esempio concreto è applicare l'oggetto ad una serie temporale per estrarre caratteristiche trigonometriche.
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(12, 4))
average_week_demand = df.groupby(["weekday", "hour"])["count"].mean()
average_week_demand.plot(ax=ax)
_ = ax.set(
title="Average hourly bike demand during the week",
xticks=[i * 24 for i in range(7)],
xticklabels=["Sun", "Mon", "Tue", "Wed", "Thu", "Fri", "Sat"],
xlabel="Time of the week",
y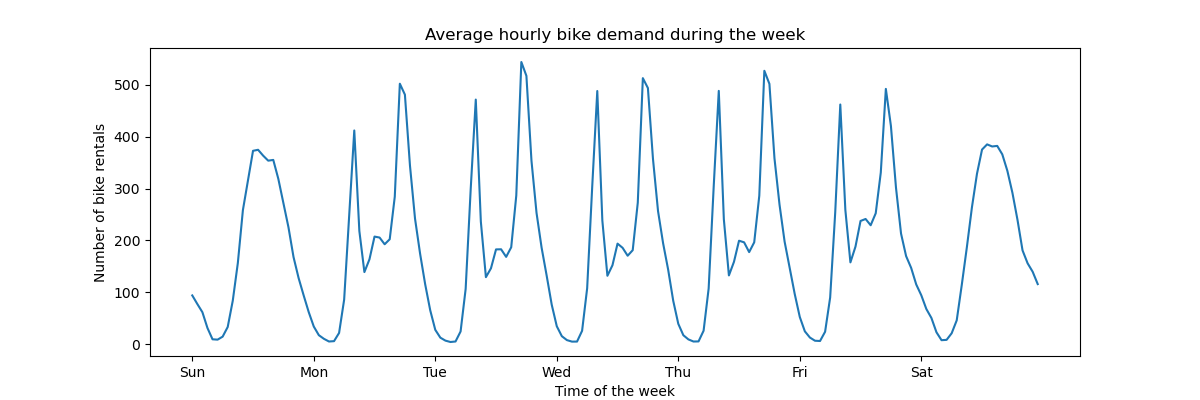
Generalmente l'utilizzo tipico di FunctionTransformer si vede nella
- creazione di feature complesse o dominio-specifiche
- applicazione di operazioni matematiche non usuali ai dati
- integrazione di logiche di preprocessing esistenti in pipeline Scikit-learn
FunctionTransformer agisce quindi come un ponte tra le funzioni Python personalizzate e quelle di Scikit-learn, offrendo flessibilità nel preprocessing dei dati e nella feature engineering.
Applicazione pratica
Applichiamo la funzione per creare trasformazioni trigonometriche alla serie temporale mostrata sopra
from sklearn.preprocessing import FunctionTransformer
def sin_transformer(period):
return FunctionTransformer(lambda x: np.sin(x / period * 2 * np.pi))
def cos_transformer(period):
return FunctionTransformer(lambda x: np.cos(x / period * 2 * np.pi))
hour_df = pd.DataFrame(
np.arange(26).reshape(-1, 1),
columns=["hour"],
)
hour_df["hour_sin"] = sin_transformer(24).fit_transform(hour_df)["hour"]
hour_df["hour_cos"] = cos_transformer(24).fit_transform(hour_df)["hour"]
hour_df.plot(x="hour")
_ = plt.title("Codifica trigonometrica per la feature "hour")Se sei interessato a saperne di più, ti suggerisco di leggere la documentazione linkata sopra alla pagina dedicata di Sklearn. Il risultato della trasformazione è visibile nel grafico qui sotto
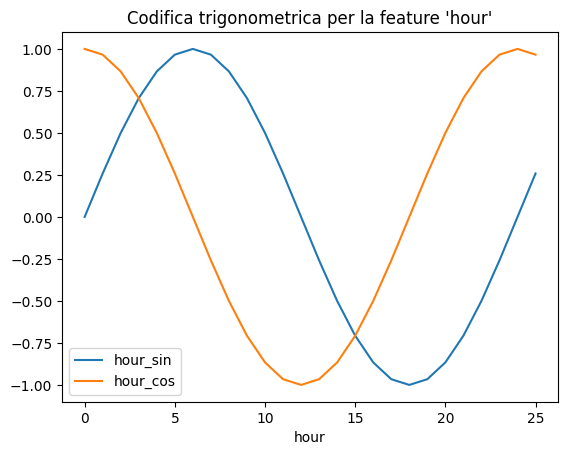
Questo è solo uno degli esempi di applicazione, proprio perché questo oggetto trova parecchio utilizzo proprio nelle serie temporali.
KBinsDiscretizer
KBinsDiscretizer è una classe di preprocessing in Scikit-learn progettata per trasformare feature continue in feature categoriche discrete. Questo processo è noto come discretizzazione, quantizzazione o binning. Alcuni set di dati con caratteristiche continue possono trarre vantaggio dalla discretizzazione, perché questa può trasformare il set di dati con attributi continui in uno con solo attributi nominali.
Il suo obiettivo è suddividere l'intervallo di una variabile continua in un numero specifico di intervalli (o bin). Ogni valore originale viene poi sostituito con l'etichetta del bin in cui cade.
L'algoritmo funziona così:
- Analizza la distribuzione della feature continua
- Crea un numero predefinito di bin basati su questa distribuzione
- Assegna ogni valore originale al bin appropriato
- Sostituisce i valori originali con le etichette dei bin o con codifiche one-hot dei bin
Parametri chiave:
n_bins: Numero di bin da creare. Può essere un intero o un array di interi per bin diversi per ogni feature.encode: Metodo di codifica dei bin (onehot, ordinal, o onehot-dense).- onehot: codifica il risultato trasformato con codifica one-hot e restituisci una matrice sparsa. Le feature ignorate sono sempre impilate a destra
- onehot-dense: codifica il risultato trasformato con codifica one-hot e restituisce un array "denso" (cioè non in formato sparso)
- ordinal: restituisce il bin codificato come valore intero
strategy: Strategia per definire i limiti dei bin (uniform, quantile, o kmeans).- uniform crea bin di uguale ampiezza
- quantile crea bin per ogni caratteristica contenenti lo stesso numero di punti
- kmeans definisce i bin usando il clustering k-means
Puoi leggere di più a questo link.
Alcune considerazioni:
- La scelta del numero di bin e della strategia può influenzare significativamente i risultati
- Può portare a perdita di informazioni, specialmente con pochi bin (come quando mettiamo a grafico un istogramma con pochi gruppi)
- Utile per algoritmi sensibili a distribuzioni non normali o a relazioni non lineari.
Applicazione Pratica
L'applicazione la vedremo vedendo le performance di una regressione lineare e di albero decisionale nell'apprendere pattern continui vs quelli discretizzati.
Creeremo un dataset finto di numeri casuali ma semi-lineari, applicheremo i modelli ai dati continui e poi a fianco lo stesso dataset ma con feature discretizzate.
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.tree import DecisionTreeRegressor
# Impostazione del generatore di numeri casuali per riproducibilità
rnd = np.random.RandomState(42)
# Creazione del dataset
X = rnd.uniform(-3, 3, size=100) # 100 punti tra -3 e 3
y = np.sin(X) + rnd.normal(size=len(X)) / 3 # Seno con rumore aggiunto
X = X.reshape(-1, 1) # Reshape per avere la forma corretta per sklearn
# Applicazione di KBinsDiscretizer
discretizer = KBinsDiscretizer(n_bins=10, encode="onehot")
X_binned = discretizer.fit_transform(X)
# Preparazione per la visualizzazione
fig, (ax1, ax2) = plt.subplots(ncols=2, sharey=True, figsize=(12, 5))
line = np.linspace(-3, 3, 1000).reshape(-1, 1) # Punti per il plotting
# Funzione per addestrare e plottare i modelli
def train_and_plot(X_train, X_plot, ax, title):
# Regressione lineare
linear_reg = LinearRegression().fit(X_train, y)
ax.plot(line, linear_reg.predict(X_plot), linewidth=2, color="green", label="Regressione lineare")
# Albero decisionale
tree_reg = DecisionTreeRegressor(min_samples_split=3, random_state=0).fit(X_train, y)
ax.plot(line, tree_reg.predict(X_plot), linewidth=2, color="red", label="Albero decisionale")
# Dati originali
ax.plot(X[:, 0], y, "o", c="k", alpha=0.5)
ax.legend(loc="best")
ax.set_xlabel("Feature di input")
ax.set_title(title)
# Plot per dati originali
train_and_plot(X, line, ax1, "Risultato prima della discretizzazione")
ax1.set_ylabel("Output della regressione")
# Plot per dati discretizzati
line_binned = discretizer.transform(line)
train_and_plot(X_binned, line_binned, ax2, "Risultato dopo la discretizzazione")
plt.tight_layout()
plt.show()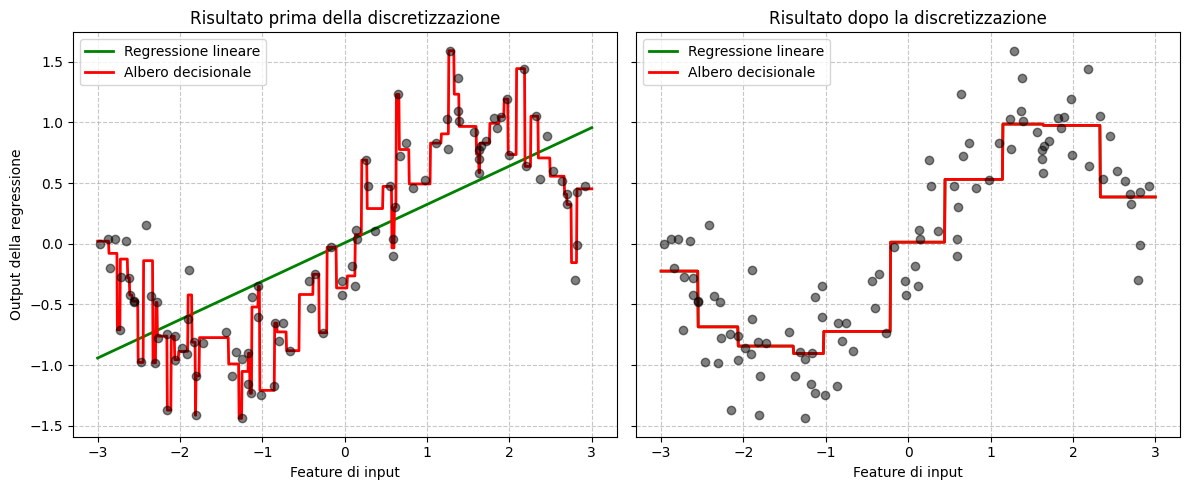
La regressione lineare migliora significativamente dopo la discretizzazione, catturando meglio la non linearità. L'albero decisionale mostra meno cambiamenti, poiché è già capace di gestire non linearità. Questo esempio illustra come la discretizzazione può aiutare modelli lineari a catturare relazioni non lineari, potenzialmente migliorando le prestazioni in alcuni scenari.

Trasformazione logaritmo
Il principale vantaggio della trasformazione logaritmica è la sua capacità di comprimere il range dei valori. Questo effetto è particolarmente utile quando si lavora con dati che presentano una grande variabilità o outlier.
Il logaritmo riduce la distanza tra i valori più grandi, mantenendo relativamente inalterati quelli più piccoli. Così facendo, normalizza le distribuzioni asimmetriche, rendendo più simmetriche quelle con coda destra e avvicinandole a una distribuzione normale.
Un altro aspetto cruciale è la sua capacità di linearizzare relazioni altrimenti non lineari. In molti casi, la trasformazione logaritmica può convertire relazioni esponenziali in lineari, semplificando l'analisi e migliorando le prestazioni di modelli che assumono linearità tra le variabili.
La sua funzione di compressione si nota quando si lavora con dati estremi e permette quindi di gestire gli outlier senza doverli rimuovere dal dataset, preservando così informazioni potenzialmente importanti.
Matematicamente, la trasformazione più comune utilizza il logaritmo naturale (base e), definito come \( y=ln(x) \), dove \( x \) è il valore originale e \( y \) quello trasformato. È importante notare che questa trasformazione è definita solo per valori positivi di \( x \), richiedendo talvolta l'aggiunta di una costante ai dati in presenza di zeri o valori negativi.
La trasformazione logaritmica può essere utilizzata come tecnica di feature scaling, complementare o alternativa a metodi come la standardizzazione o la normalizzazione min-max. Inoltre, può migliorare le prestazioni di modelli specifici, come la regressione lineare, che beneficiano di feature con distribuzioni più simmetriche.
Applicazione Pratica
Nel machine learning, la log transform si usa la maggior parte delle volte quando si vuole normalizzare una distribuzione non naturalmente distribuita.
Ad esempio, una nota variabile non normalmente distribuita è quella del guadagno annuale - spesso si vuole modellare questa variabile per fornire predizioni di valore, ma lavorare con questa distribuzione non è conveniente, soprattutto se si usano algoritmi che non modellano correttamente dati non lineari.
Con una trasformazione logartimo, attraverso numpy, è possibile tendere alla distribuzione normale, rendendo la variabile più facilmente prevedibile.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Creiamo un dataset di esempio con valori positivamente asimmetrici
np.random.seed(42)
data = {
'Income': np.random.exponential(scale=50000, size=1000) # distribuzione esponenziale per simulare la skewness
}
df = pd.DataFrame(data)
# Creazione di una figura con due sottografici fianco a fianco
fig, axes = plt.subplots(1, 2, figsize=(15, 5))
# Grafico della distribuzione originale
axes[0].hist(df['Income'], bins=50, color='blue', alpha=0.7)
axes[0].set_title('Distribuzione originale di Income')
axes[0].set_xlabel('Income')
axes[0].set_ylabel('Frequenza')
# Applicazione della trasformazione logaritmica
df['Log_Income'] = np.log1p(df['Income']) # log1p è equivalente a log(x + 1)
# Grafico della distribuzione trasformata
axes[1].hist(df['Log_Income'], bins=50, color='green', alpha=0.7)
axes[1].set_title('Distribuzione logaritmica di Income')
axes[1].set_xlabel('Log_Income')
axes[1].set_ylabel('Frequenza')
# Mostra il grafico
plt.tight_layout()
plt.show()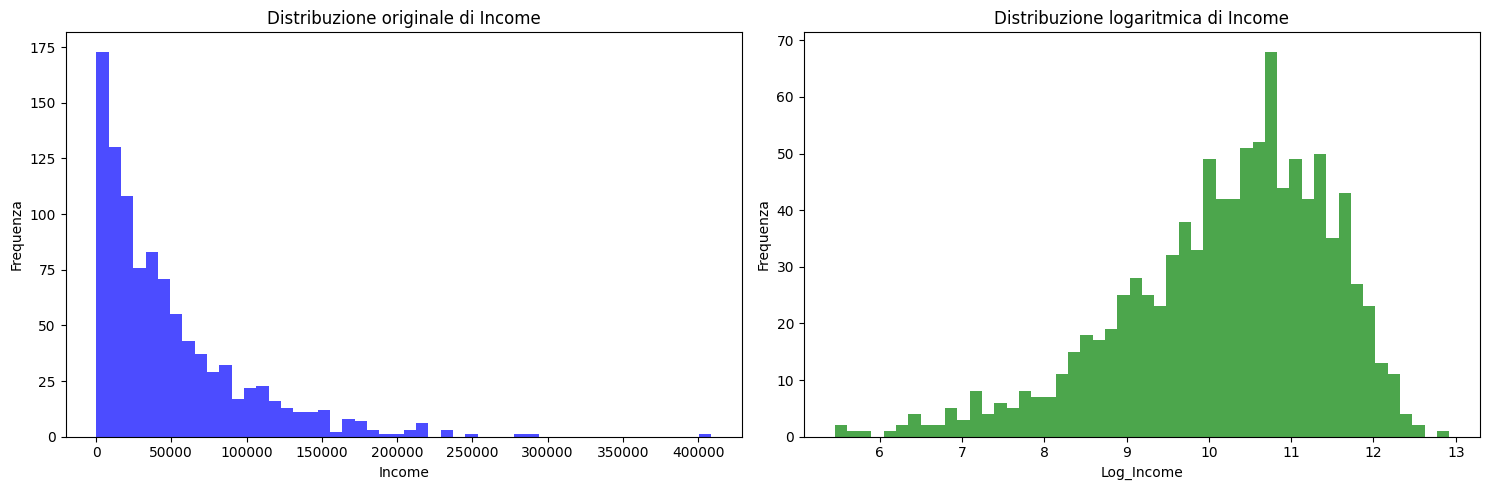
PowerTransformer
PowerTransformer è un modulo di Sklearn preprocessing che contiene logiche usate per rendere i dati più simili a quelli gaussiani. Ciò è utile per modellare problemi correlati all'eteroschedasticità (quindi di varianza non costante) o altre situazioni in cui è desiderata la normalità.
Attualmente, PowerTransformer supporta la trasformazione Box-Cox e quella Yeo-Johnson. Il parametro ottimale per stabilizzare la varianza e minimizzare l'asimmetria viene stimato tramite la massima verosimiglianza (log likelihood).
Box-Cox richiede che i dati di input siano rigorosamente positivi, mentre Yeo-Johnson supporta sia dati positivi che negativi.
Nel contesto del machine learning, queste trasformazioni affrontano diverse sfide comuni:
- Normalizzazione dei dati: Molti algoritmi di machine learning, come la regressione lineare, le reti neurali e alcuni metodi di clustering, assumono che i dati seguano una distribuzione normale.
PowerTransformerpuò trasformare distribuzioni asimmetriche o con code pesanti in forme più vicine alla gaussiana, migliorando le prestazioni di questi modelli - Stabilizzazione della varianza: In dataset reali, la varianza delle feature spesso cambia al variare della loro magnitudine. Questo fenomeno, chiamata eteroschedasticità, può compromettere l'efficacia di molti algoritmi.
- Linearizzazione delle relazioni: Alcuni algoritmi, come la regressione lineare, assumono relazioni lineari tra le variabili.
PowerTransformerpuò linearizzare relazioni non lineari, ampliando l'applicabilità di questi modelli a dataset complessi.
Partiamo prima dalla trasformazione Box-Cox, che è matematicamente definita come:
\[ y(\lambda) = \begin{cases} \frac{y^\lambda - 1}{\lambda}, & \text{se} \lambda \neq 0 \\ \ln(y), & \text{se} \lambda = 0 \end{cases} \]
dove \( x \) è il valore originale e \( \lambda \) è il parametro di trasformazione che viene inferito a livello algoritmico.
PowerTransformer si comporta come un Estimator di Sklearn e supporta il metodo .fit() e .transform().Non andrò nel dettaglio invece della transform Yeo-Johnson - sappiate solo che si basa sulla Box-Cox e permette i valori negativi.
Applicazione Pratica
Come menzionato, la transform Yeo-Johnson si basa sulla Box-Cox, ma il valore che può assumere lambda può cambiare. Questo rende le trasformazioni essenzialmente diverse in quanto possono dare risultati diversi.
In Python, basta passare uno dei tuoi metodi di trasformazione come stringa nell'oggetto PowerTransformer
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PowerTransformer
# Genera dati con valori sia positivi che negativi
np.random.seed(42)
data_positive = np.random.exponential(scale=2, size=1000)
data_negative = -np.random.exponential(scale=0.5, size=200)
data = np.concatenate([data_positive, data_negative])
# Crea due istanze di PowerTransformer, una per Yeo-Johnson e una per Box-Cox per metterli a confronto
pt_yj = PowerTransformer(method='yeo-johnson', standardize=False)
pt_bc = PowerTransformer(method='box-cox', standardize=False)
# Applica le trasformazioni
data_yj = pt_yj.fit_transform(data.reshape(-1, 1))
# Box-Cox richiede dati positivi, quindi aggiungiamo un offset per renderli tutti positivi
data_offset = data - np.min(data) + 1e-6
data_bc = pt_bc.fit_transform(data_offset.reshape(-1, 1))
# Visualizza i risultati
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(18, 5))
ax1.hist(data, bins=50, edgecolor='black')
ax1.set_title("Dati originali")
ax1.set_xlabel("Valore")
ax1.set_ylabel("Frequenza")
ax2.hist(data_yj, bins=50, edgecolor='black')
ax2.set_title("Trasformazione Yeo-Johnson")
ax2.set_xlabel("Valore")
ax3.hist(data_bc, bins=50, edgecolor='black')
ax3.set_title("Trasformazione Box-Cox")
ax3.set_xlabel("Valore")
plt.tight_layout()
plt.show()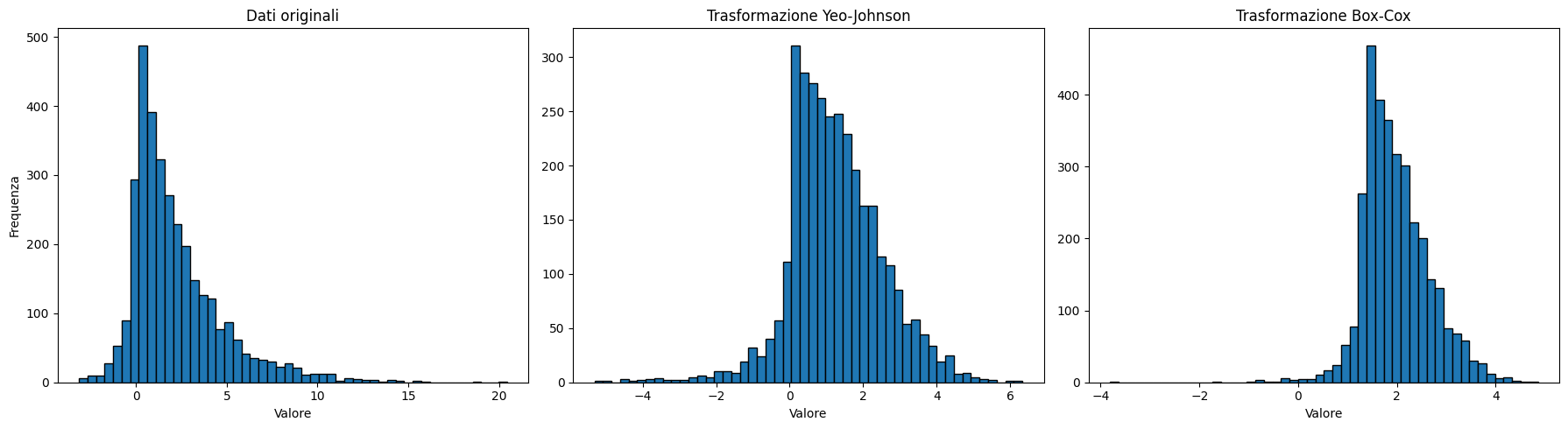
QuantileTransformer
Una trasformazione quantile mappa la distribuzione di una variabile ad un'altra distribuzione di destinazione. Attraverso la classe QuantileTransformer di Sklearn, è possibile convertire una distribuzione non normale in una distribuzione desiderata.
Consideriamo qualsiasi distribuzione di eventi - ogni evento di questa distribuzione avrà associato ad esso una probabilità che esso accada. Questo comportamento viene definito dalla distribuzione di probabilità cumulativa (cumulative density function, CDF), che varia per ogni distribuzione.
La funzione quantile è l'inverso della CDF: mentre una CDF è una funzione che restituisce la probabilità di un valore pari o inferiore a un valore dato, la PPF è l'inversa di questa funzione e restituisce il valore pari o inferiore a una probabilità data.
Nel contesto del rilevamento di valori anomali, QuantileTransformer può essere utilizzato per trasformare i dati in modo da renderli più visibili. Trasformando i dati in una distribuzione uniforme, i valori anomali verranno mappati agli estremi della distribuzione, rendendoli più distinguibili dagli inlier.
Il QuantileTransformer può forzare qualsiasi distribuzione arbitraria in una gaussiana, a condizione che ci siano sufficienti campioni di training (migliaia). Poiché è un metodo non parametrico, è più difficile da interpretare rispetto a quelli parametrici (Box-Cox e Yeo-Johnson).
Applicazione pratica
Sklearn ci viene in aiuto nuovamente con l'oggetto dedicato QuantileTransformer con un parametro importante: output_distribution, che può accettare i valori "uniform" o "normal". Queste rappresentano la distribuzione a cui vengono mappati i dati.
import numpy as np
from sklearn.preprocessing import QuantileTransformer
import matplotlib.pyplot as plt
# Creiamo un dataset di esempio con una distribuzione distorta
np.random.seed(0)
data = np.random.exponential(scale=2, size=(1000, 1)) # Distribuzione esponenziale
# Inizializziamo il QuantileTransformer
quantile_transformer = QuantileTransformer(n_quantiles=100, output_distribution='normal')
# Applichiamo la trasformazione
data_transformed = quantile_transformer.fit_transform(data)
# Visualizzazione dei dati originali e trasformati
plt.figure(figsize=(12, 6))
# Istogramma dei dati originali
plt.subplot(1, 2, 1)
plt.hist(data, bins=50, color='blue', edgecolor='black')
plt.title("Dati originali (esponenziali)")
# Istogramma dei dati trasformati
plt.subplot(1, 2, 2)
plt.hist(data_transformed, bins=50, color='green', edgecolor='black')
plt.title("Dati trasformati (normali)")
plt.show()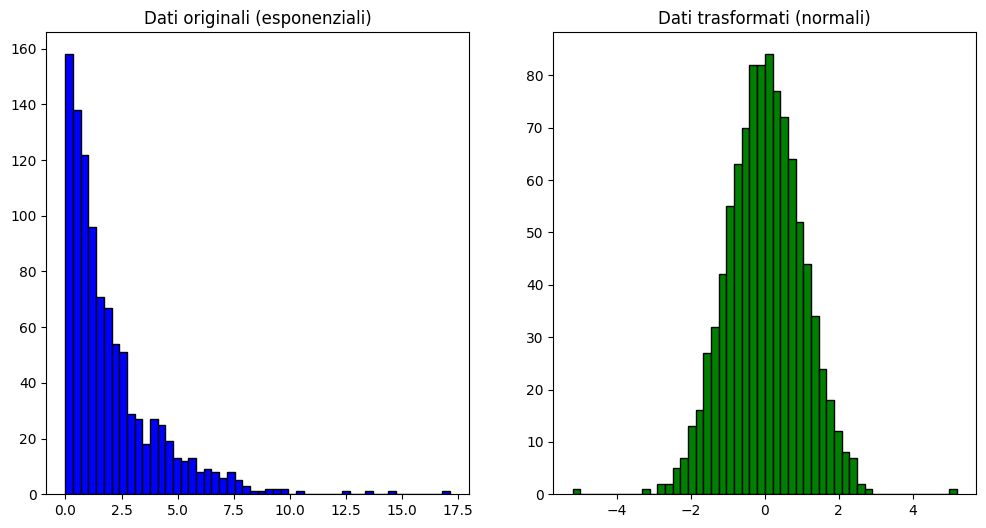
Esempi di trasformazioni: da distribuzioni specifiche alla normale
Di seguito una visualizzazione grafica che mette a confronto diverse distribuzioni non normali e la loro relativa trasformazione, passando per alcune delle tecniche da noi esplorate.
Ho usato come riferimento l'immagine presente alla documentazione di Sklearn, modificando le label per l'italiano e l'ordinamento dei grafici per una lettura più semplice.
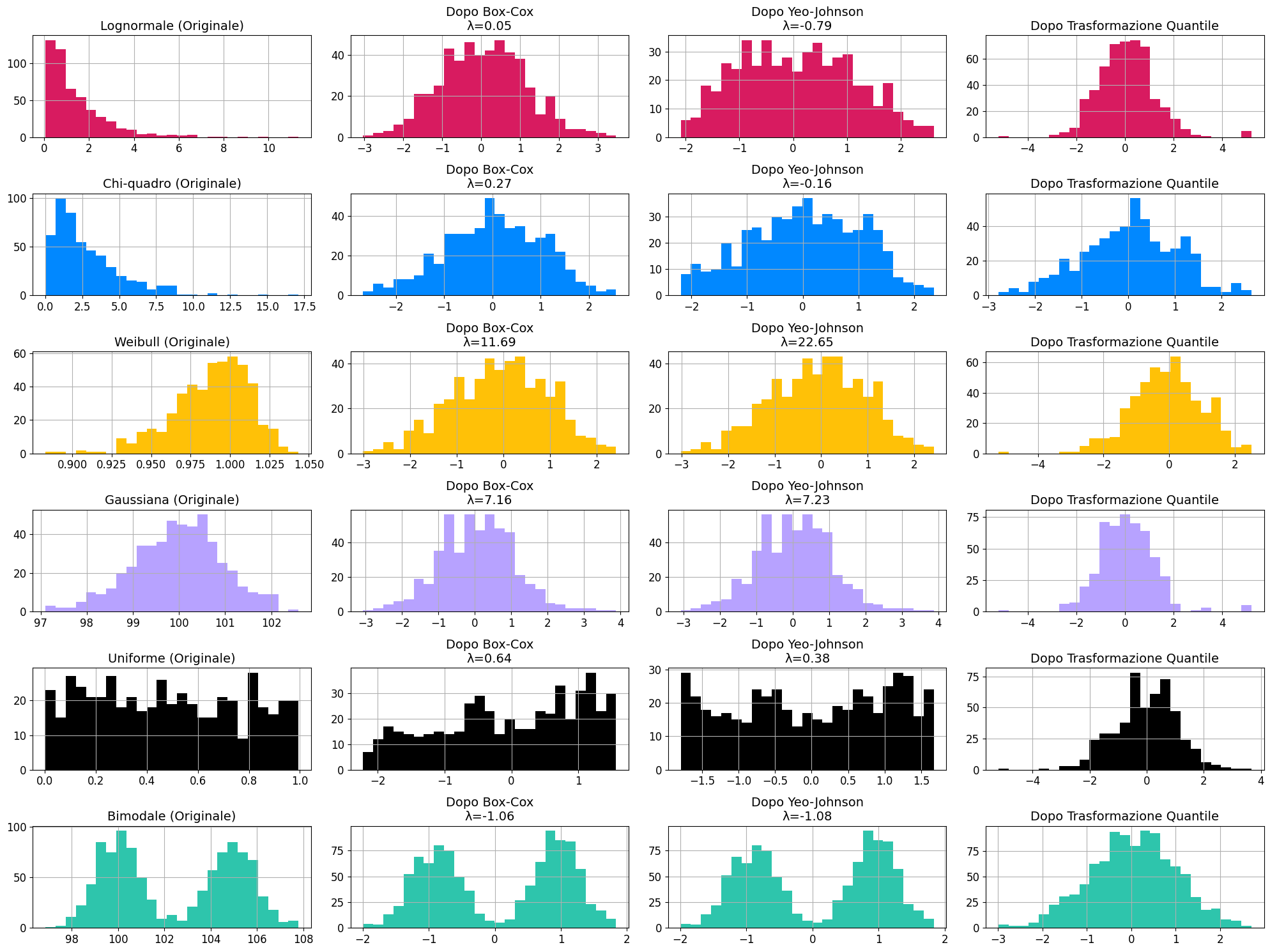
Questa immagine fa notare il limite di alcune trasformazioni, che non sempre riescono nel loro intento. Ad esempio, per la distribuzione bimodale, tutte i tentativi di trasformazione verso la curva normale falliscono tranne la trasformazione quantile.
Principal Component Analysis
La PCA trasforma un set di variabili possibilmente correlate in un set di variabili linearmente non correlate chiamate componenti principali. Queste componenti principali sono ordinate in modo che le prime contengano la maggior parte della varianza presente nelle variabili originali.
Ho scritto un articolo dettagliato su cosa sia la PCA se ti interessa 👇

Nel contesto del feature engineering, la PCA può essere usata per ridurre il numero di feature mantenendo la maggior parte dell'informazione. Questo riduce potenzialmente il rumore presente nei dati e correlazioni poco rilevanti che potrebbero confondere il modello.
Essendo una tecnica di riduzione della dimensionalità, la PCA andrebbe usata per comprimere il dataset anziché espanderlo. la PCA può estrarre alcune caratteristiche latenti, che sono fattori nascosti o sottostanti che influenzano i tuoi dati.
Ad esempio, se hai un set di dati di immagini, puoi usare la PCA per trovare caratteristiche che rappresentano la forma, il colore o la consistenza degli oggetti nelle immagini. Queste caratteristiche latenti possono aiutarti a comprendere meglio i tuoi dati e a migliorare i tuoi modelli di apprendimento automatico.
Applicazione pratica
Una applicazione della PCA come feature engineering si ha lavorando con le immagini e quindi nella computer vision.
Prendiamo volti a caso presenti all'interno del dataset lfw_people di Sklearn. È possibile usare TruncatedSVD (una tecnica di compressione molto simile alla PCA) per estrarre caratteristiche fondamentali dell'immagine, come contorni, ombre e posizione degli oggetti principali per fornire al modello di machine learning informazioni rilevanti per la modellazione.
Una applicazione tipica di questo approccio è quella di normalizzare le immagini, rendendo il sistema più robusto a variazioni di illuminazione o altre condizioni - questo rende le facce ridotte una base per un eventuale riconoscimento facciale.
Chiaramente questo approccio è applicabile a dati anche tabellari.

Codice Python per creare questa visualizzazione:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_lfw_people
from sklearn.decomposition import TruncatedSVD
# Carica il dataset Labeled Faces in the Wild
lfw_people = fetch_lfw_people(min_faces_per_person=70, resize=0.4)
X = lfw_people.data
n_samples, h, w = lfw_people.images.shape
print(f"Dimensioni del dataset: {X.shape}")
# Numero di componenti da utilizzare per la riduzione
n_components = 50
# Applica TruncatedSVD
svd = TruncatedSVD(n_components=n_components, random_state=42)
X_transformed = svd.fit_transform(X)
# Funzione per ricostruire un'immagine
def reconstruct_image(svd, X_transformed):
return np.dot(X_transformed, svd.components_)
# Ricostruisci tutte le immagini
X_reconstructed = reconstruct_image(svd, X_transformed)
# Funzione per visualizzare i volti originali e ridotti in modo trasposto
def plot_transposed_original_and_reduced(X_original, X_reduced, n_faces=5):
fig, axes = plt.subplots(2, n_faces, figsize=(3*n_faces, 6))
random_indices = np.random.choice(X_original.shape[0], n_faces, replace=False)
for i, idx in enumerate(random_indices):
# Volto originale
axes[0, i].imshow(X_original[idx].reshape(h, w), cmap='gray')
axes[0, i].set_title(f'Volto {i+1}\nOriginale')
axes[0, i].axis('off')
# Volto ridotto
axes[1, i].imshow(X_reduced[idx].reshape(h, w), cmap='gray')
axes[1, i].set_title(f'Ridotto\n({n_components} comp.)')
axes[1, i].axis('off')
plt.tight_layout()
plt.show()
# Visualizza i volti originali e ridotti in modo trasposto
plot_transposed_original_and_reduced(X, X_reconstructed)
# Calcola e stampa l'errore di ricostruzione medio
mse = np.mean((X - X_reconstructed) ** 2)
print(f"\nErrore di ricostruzione medio (MSE): {mse:.4f}")
# Stampa la varianza spiegata cumulativa
explained_variance_ratio = svd.explained_variance_ratio_
cumulative_variance_ratio = np.cumsum(explained_variance_ratio)
print(f"\nVarianza spiegata cumulativa con {n_components} componenti: {cumulative_variance_ratio[-1]:.4f}")
# Visualizza le prime componenti
n_components_show = min(10, n_components)
components = svd.components_[:n_components_show].reshape((n_components_show, h, w))
fig, axes = plt.subplots(2, 5, figsize=(15, 6))
for i, ax in enumerate(axes.flat):
if i < n_components_show:
ax.imshow(components[i], cmap='gray')
ax.set_title(f'Componente {i+1}')
ax.axis('off')
plt.tight_layout()
plt.show()Conclusione
Questo articolo ha esplorato diverse tecniche avanzate di feature engineering per dati numerici, evidenziando il loro ruolo cruciale nel migliorare le prestazioni dei modelli di machine learning. Le metodologie discusse includono:
- Normalizzazione
- Feature polinomiali
- FunctionTransformer
- KBinsDiscretizer
- Trasformazione logaritmica
- PowerTransformer (Box-Cox e Yeo-Johnson)
- QuantileTransformer
- PCA
Ogni tecnica offre vantaggi specifici e si adatta a particolari tipi di dati e problemi. La scelta della trasformazione più appropriata dipende dalla natura dei dati, dal problema da affrontare e dal modello selezionato. Non esiste una soluzione universale, rendendo fondamentali la sperimentazione e la validazione.








Commenti dalla community