In questo articolo vedremo come fare una previsione da una serie temporale con Tensorflow e Keras in Python. Useremo una rete neurale sequenziale creata in Tensorflow basata su strati LSTM bidirezionali per catturare i pattern nelle sequenze univariate che daremo in input al modello.
In particolare vedremo come
- generate dei dati sintetici per simulare una serie temporale con diverse caratteristiche
- processare i dati in set di addestramento e validazione e creare un dataset basato su finestre temporali
- definire una architettura per la nostra rete neurale usando LSTM (long short-term memory)
- addestrare e valutare il modello
L'obiettivo di questo tutorial è quello di predire un punto nel futuro data una sequenza di dati. Non verrà coperto il caso multi-step - quello dove si fa previsione del punto precedente che è a sua volta stato generato dal modello.
Iniziamo.
Generazione dei dati
Invece di scaricare un dataset dal web, useremo delle funzioni che ci permetteranno di generare delle serie temporali plausibili e usabili per il nostro caso. Useremo anche dataclass per memorizzare i parametri della nostra serie temporale in una classe così da poterla usare a prescindere dallo scope. Il nome della dataclass sarà G, che sta per "globale".
Ho deciso di usare questo approccio invece di usare un dataset vero e proprio perché questa metodica ci permette di testare più serie temporali e avere flessibilità nel processo creativo dei nostri progetti.
def plot_series(time, series, format="-", start=0, end=None):
"""Funzione helper per plottare il grafico della serie temporale"""
plt.plot(time[start:end], series[start:end], format)
plt.xlabel("Time")
plt.ylabel("Value")
plt.grid(False)
def trend(time, slope=0):
"""Definizione di un trend attraverso pendenza e tempo"""
return slope * time
def seasonal_pattern(season_time):
"""Definizione arbitraria di un pattern di stagionalità"""
return np.where(season_time < 0.1,
np.cos(season_time * 6 * np.pi),
2 / np.exp(9 * season_time))
def seasonality(time, period, amplitude=1, phase=0):
"""Ripete un pattern a ogni periodo"""
season_time = ((time + phase) % period) / period
return amplitude * seasonal_pattern(season_time)
def noise(time, noise_level=1, seed=None):
"""Aggiunge rumore bianco alla serie"""
rnd = np.random.RandomState(seed)
return rnd.randn(len(time)) * noise_levelGeneriamo una serie temporale sintetica con questo codice
def generate_time_series():
# La dimensione temporale: 4 anni di dati
time = np.arange(4 * 365 + 1, dtype="float32")
# La serie iniziale non è altro che una linea retta che poi andremo a modificare con le altre funzioni
y_intercept = 10
slope = 0.005
series = trend(time, slope) + y_intercept
# Aggiungiamo stagionalità
amplitude = 50
series += seasonality(time, period=365, amplitude=amplitude)
# Aggiungiamo rumore
noise_level = 3
series += noise(time, noise_level, seed=51)
return time, series
# Salviamo i parametri della nostra serie temporale
@dataclass
class G:
TIME, SERIES = generate_time_series()
SPLIT_TIME = 1100 # al giorno 1100 finirà il periodo di training. Il resto sarà set di validazione
WINDOW_SIZE = 20 # quanti giorni prenderemo in considerazione per fare la nostra previsione
BATCH_SIZE = 32 # quanti item forniremo per batch
SHUFFLE_BUFFER_SIZE = 1000 # questo parametro ci serve per definire il buffer di campionatura di Tensorflow
# plottiamo la serie sintetica
plt.figure(figsize=(10, 6))
plot_series(G.TIME, G.SERIES)
plt.show()La serie ottenuta è la seguente
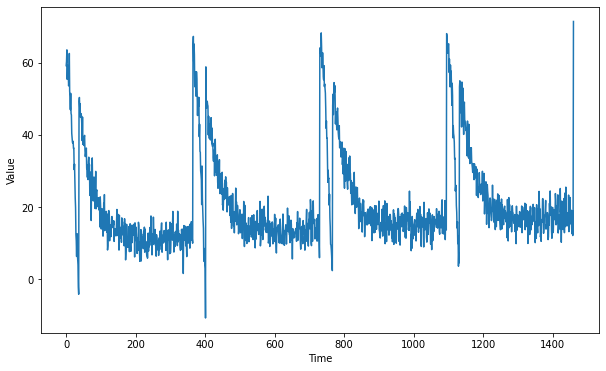
Ora che abbiamo una serie temporale usabile, passiamo al preprocessing.
Preprocessing della serie temporale per il deep learning
La particolarità delle serie temporali è che devono essere divise in set di training e validazione e che a loro volta devono essere divise in sequenze di una lunghezza definita dalla nostra configurazione. Queste sequenze si chiamano finestre (windows) e il modello userà proprio queste sequenze per produrre una previsione.
Vediamo altre due funzioni helper per raggiungere questo obiettivo.
Qui sono dovute alcune spiegazioni. La funzione train_val_split non fa altro che dividere la nostra serie in base al valore G.SPLIT_TIME definito precedentemente nella dataclass G. Inoltre, gli passeremo i parametri G.TIME e G.SERIES.
Rammentiamo la definizione della dataclass G.

In base generate_time_series,
TIME = range(0, 1439)
SERIES = array([ 0.81884814, 0.82252744, 0.77998762, ..., -0.44389692, -0.42693424, -0.39230758])
Entrambi di lunghezza 1439.
La divisione di train_val_split sarà quindi uguale a
time_train = range(0, 1100)
time_val = range(1100, 1439)
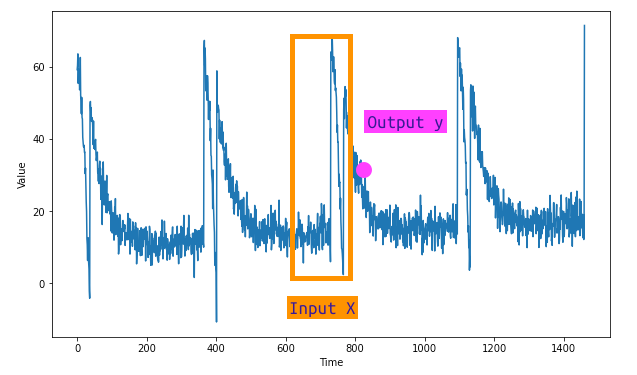
Dopo aver diviso in set di training e validazione useremo delle funzioni di Tensorflow per creare un oggetto Dataset che permetterà di creare le feature X e il target y. Ricordiamo che X sono gli n valori che il modello userà per predire il prossimo, che sarebbe la y.
Vediamo come implementare queste funzioni
def train_val_split(time, series, time_step=G.SPLIT_TIME):
"""Dividere la serie temporale in training e validation set"""
time_train = time[:time_step]
series_train = series[:time_step]
time_valid = time[time_step:]
series_valid = series[time_step:]
return time_train, series_train, time_valid, series_valid
def windowed_dataset(series, window_size=G.WINDOW_SIZE, batch_size=G.BATCH_SIZE, shuffle_buffer=G.SHUFFLE_BUFFER_SIZE):
"""
Creiamo delle finestre temporali per creare delle feature X e y.
Se ad esempio scegliamo una finestra di 30, creeremo un dataset formato da 30 punti come X
"""
dataset = tf.data.Dataset.from_tensor_slices(series)
dataset = dataset.window(window_size + 1, shift=1, drop_remainder=True)
dataset = dataset.flat_map(lambda window: window.batch(window_size + 1))
dataset = dataset.shuffle(shuffle_buffer)
dataset = dataset.map(lambda window: (window[:-1], window[-1]))
dataset = dataset.batch(batch_size).prefetch(1)
return datasetUseremo il metodo .window() di Tensorflow sull’oggetto dataset per applicare uno shift di 1 ai nostri punti. Un esempio della logica applicata può essere visto qui:
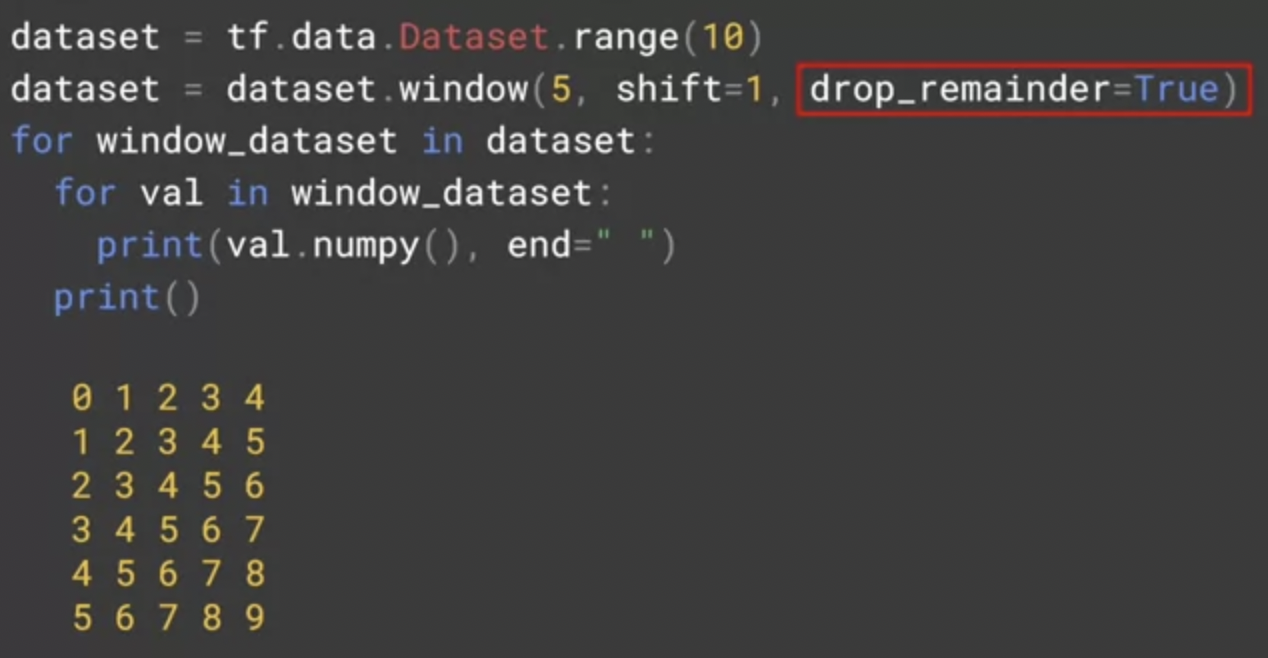
Nell’esempio creiamo un range da 0 a 10 con Tensorflow, e applichiamo una window di 5. Si creeranno quindi un totale di 5 colonne. Passando shift=1 ogni colonna avrà un valore in meno partendo dall’alto (shiftato) e drop_remainder=True assicurerà di avere una matrice sempre della stessa dimensione.
Applichiamo queste due funzioni.
# creiamo il dataset con finestre temporali
dataset = windowed_dataset(series_train)
# dividiamo in training e validation set
time_train, series_train, time_valid, series_valid = train_val_split(G.TIME, G.SERIES)Ora che i dati sono pronti possiamo dedicarci a strutturare la nostra rete neurale.
Architettura della rete neurale
Come menzionato all’inizio dell’articolo, la nostra rete neurale si baserà prevalentemente su strati LSTM (long-short term memory). Quello che rende una LSTM adatta a questo tipo di compito è che possiede un struttura interna in grado di propagare le informazioni attraverso lunghe sequenze. Questo le rende molto utili nell’elaborazione del linguaggio naturale (NLP) e per l’appunto nelle serie temporali, proprio perché questi due tipi di compiti potrebbero richiedere di trasferire informazioni durante l’intera sequenza.
Nel codice che segue vedremo come gli strati LSTM siano inclusi all’interno di uno strato Bidirectional. Questo strato permette alla LSTM di considerare la sequenza di dati in entrambe le direzioni e di poter quindi avere contesto non solo del passato ma anche del futuro. Ci aiuterà a costruire una network che sarà più precisa rispetto a una unidirezionale.
Oltre alle LSTM esistono anche le GRU (Gated Recurrent Units) che possono essere impiegate per task di predizione delle serie temporali.
Useremo anche lo strato Lambda che ci permetterà di adattare correttamente il formato dei dati in input alla nostra rete e infine uno strato denso per calcolare l’output finale.
Vediamo come implementare tutto questo in Keras e Tensorflow in maniera sequenziale.
Lo strato Lambda permette di usare delle funzioni custom all’interno di uno strato. Lo usiamo per assicurarci che la dimensionalità dell’input sia adeguata alla LSTM. Poiché il nostro dataset è composto finestre temporali bidimensionali, dove la prima è la batch_size e l’altra è timesteps.
Una LSTM però accetta una terza dimensione, che indica il numero di dimensioni del nostro input. Usando la funzione Lambda e input_shape = [None], stiamo di fatto dicendo a Tensorflow di accettare qualsiasi tipo di dimensione in input. Questo è comodo perché non dobbiamo scrivere codice aggiuntivo per assicurare che la dimensionalità sia corretta.
Per leggere di più su LSTM e come funziona il layer, invito il lettore a consultare la guida ufficiale di Tensorflow presente qui.
Tutti gli strati LSTM sono inclusi all’interno di uno strato Bidirezionale, e ognuna di esse passa le sequenze elaborate al prossimo strato attraverso return_sequences = True. Se questo argomento fosse falso, Tensorflow darebbe errore, poiché lo strato LSTM successivo non troverebbe una sequenza da processare. L’unico strato che non deve restituire le sequenze è l’ultimo LSTM, poiché lo strato denso finale è quello deputato a fornire la predizione finale e non un’altra sequenza.
La callback EarlyStopping
Come è possibile leggere nell’articolo Controllare il training di una rete neurale in Tensorflow, useremo una callback per fermare il training quando la nostra metrica di performance raggiunge un livello specificato. Useremo il MAE (Mean absolute error) per misurare quanto la nostra network sia in grado di predire correttamente il prossimo punto della serie.
Di fatto, questo è un compito simile ad un task di regressione, e quindi userà delle metriche di performance analoghe.
Vediamo il codice per implementare l’early stopping
def create_uncompiled_model():
# definiamo un modello sequenziale
model = tf.keras.models.Sequential([
tf.keras.layers.Lambda(lambda x: tf.expand_dims(x, axis=-1),
input_shape=[None]),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(1024, return_sequences=True)),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(512, return_sequences=True)),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(256, return_sequences=True)),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(128, return_sequences=True)),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(64)),
tf.keras.layers.Dense(1),
])
return modelAddestramento del modello
Siamo pronti ad addestrare il nostro modello LSTM. Definiamo una funzione che andrà a chiamare create_uncompiled_model e andrà a fornire al modello una funzione di perdita e un ottimizzatore.
La funzione di perdita di Huber può essere utilizzata per bilanciare tra l'errore medio assoluto, o MAE, e l'errore quadratico medio, MSE. È quindi una buona funzione di perdita per quando si hanno dati vari o solo pochi valori anomali, come in questo caso.
L’ottimizzatore Adam è una scelta generalmente valida - settiamo un learning_rate arbitrario di 0.001.
def create_model():
tf.random.set_seed(51)
model = create_uncompiled_model()
model.compile(loss=tf.keras.losses.Huber(),
optimizer=tf.keras.optimizers.Adam(learning_rate=0.001),
metrics=["mae"])
return model
model = create_model()
# addestriamo per 20 epochs con e assegnamo la callback
history = model.fit(dataset, epochs=20, callbacks=[early_stopping])Lanciamo il training

Vediamo come alla 20° epoca il MAE target viene raggiunto e il training viene stoppato.
Valutazione del modello
Plottiamo le curve per la loss e il MAE.
# plottiamo MAE e loss
plt.figure(figsize=(10, 6))
plt.plot(history.history['mae'], label='mae')
plt.plot(history.history['loss'], label='loss')
plt.legend()
plt.show()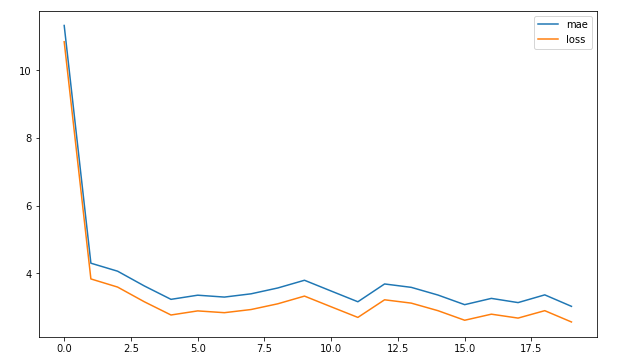
Le curve mostrano un miglioramento della net fino a stabilizzarsi già dopo la 5° epoca. È comunque un buon risultato.
Usiamo una funzione helper per un facile accesso a MAE e MSE. Inoltre, definiamo anche una funzione per creare le previsioni.
def compute_metrics(true_series, forecast):
"""Helper per stampare MSE e MAE"""
mse = tf.keras.metrics.mean_squared_error(true_series, forecast).numpy()
mae = tf.keras.metrics.mean_absolute_error(true_series, forecast).numpy()
return mse, mae
def model_forecast(model, series, window_size):
"""Questa funzione converte la serie in input in un Dataset con finestre temporali per la previsione"""
ds = tf.data.Dataset.from_tensor_slices(series)
ds = ds.window(window_size, shift=1, drop_remainder=True)
ds = ds.flat_map(lambda w: w.batch(window_size))
ds = ds.batch(32).prefetch(1)
forecast = model.predict(ds)
return forecastVediamo ora come si comporta il modello! Facciamo delle previsioni sulla serie intera e sul set di validazione.
# Predizione su tutta la serie temporale
all_forecast = model_forecast(model, G.SERIES, G.WINDOW_SIZE).squeeze()
# Porzione di validazione
val_forecast = all_forecast[G.SPLIT_TIME - G.WINDOW_SIZE:-1]
# Grafico
plt.figure(figsize=(10, 6))
plt.plot(series_valid, label="validation set")
plt.plot(val_forecast, label="predicted")
plt.xlabel("Timestep")
plt.ylabel("Value")
plt.legend()
plt.show()Vediamo i risultati sul set di validazione
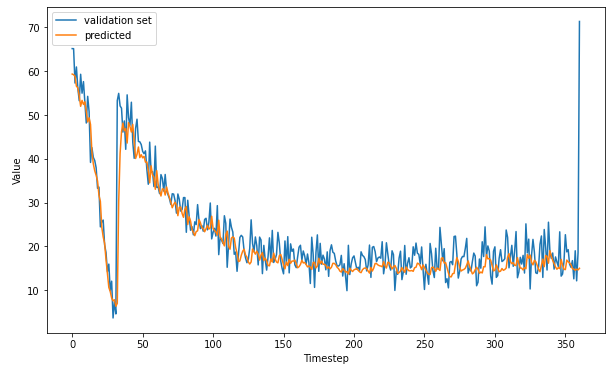
E sull'intera serie
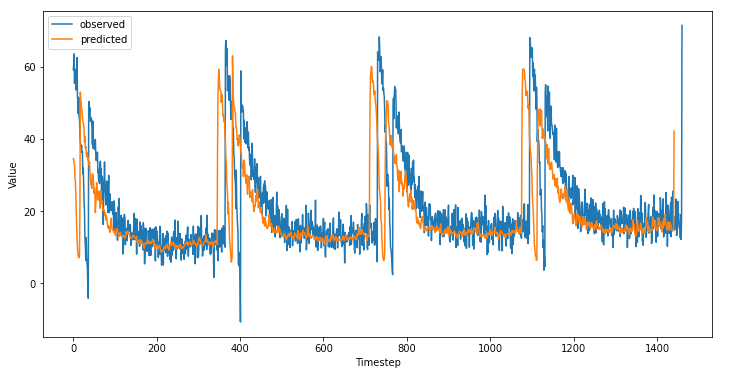
I risultati sembrano essere buoni. Forse abbiamo modo di aumentare le performance del modello aumentando le epoche di addestramento oppure giocando con il learning rate.
mse, mae = compute_metrics(series_valid, val_forecast)
print(f"mse: {mse:.2f}, mae: {mae:.2f}")mse: 30.91, mae: 3.32 forecast.
Predire un nuovo punto nel futuro
Vediamo ora come predire un punto nel futuro data l'ultima sequenza nella serie.
new_forecast = []
new_forecast_series = G.SERIES[-G.WINDOW_SIZE:]
pred = model.predict(new_forecast_series[np.newaxis])
plt.figure(figsize=(15, 6))
plt.plot(G.TIME[-100:], G.SERIES[-100:], label="last 100 points of time series")
plt.scatter(max(G.TIME)+1, pred, color="red", marker="x", s=70, label="prediction")
plt.legend()
plt.show()Ed ecco il risultato
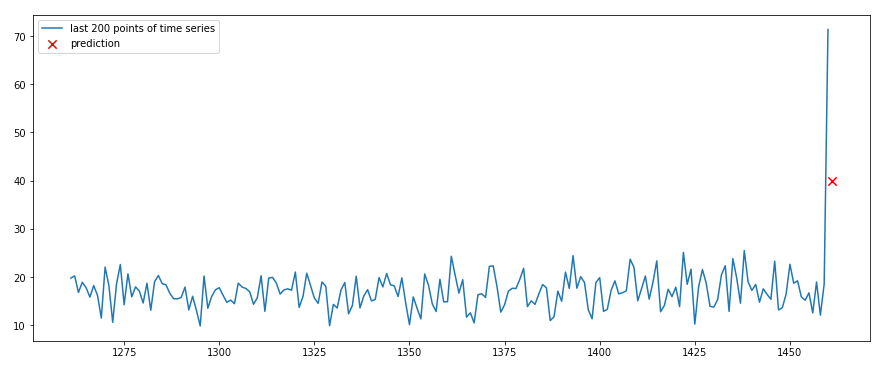
Conclusione
Ricapitolando, abbiamo visto come
- generare una serie temporale sintetica
- dividere appropriatamente la serie in X e y
- strutturare una rete neurale in Keras e Tensorflow basata su LSTM bidirezionali
- addestrare con early stopping e valutare le performance
- fare previsioni sulla serie di addestramento, validazione e nel futuro
Se avete suggerimenti su come migliorare questo flusso, scrivete nei commenti e condividete il vostro metodo. Spero che l'articolo vi possa aiutare con i vostri progetti.
A presto,







Commenti dalla community