Introduzione ai sistemi di raccomandazione content-based

Quante volte ci siamo ritrovati a scorrere all’infinito sui social, incapaci di smettere? Ogni volta che mi capita, mi ripeto che sono in balìa dell’algoritmo. Dai video verticali di TikTok e Instagram ai suggerimenti su YouTube, i contenuti che vediamo non sono casuali: ci vengono proposti perché l’algoritmo ha imparato a conoscere i nostri gusti, le nostre abitudini e ciò che ci tiene incollati allo schermo.

Ma i sistemi di raccomandazione non si limitano ai social media. Li troviamo ovunque: nelle piattaforme di streaming come Netflix e Spotify, negli e-commerce come Amazon, persino nelle app di lettura e nei siti di news. Il loro obiettivo? Offrirci consigli personalizzati basati sul nostro comportamento, aumentando il nostro coinvolgimento e spingendoci a trascorrere più tempo sulla piattaforma.

Ad esempio l'infinita spirale di contenuti consigliati: mentre mi perdo tra un video sul fantacalcio e le ultime tendenze social, mi rendo conto che l'algoritmo sa più di me circa i miei gusti. E come se non bastasse, YouTube ha deciso che la mia "serata di calcio" non è completa senza un po’ di cultura cinematografica con Criticoni (sì, sono un grande appassionato), seguita da una reaction all'album di Marracash — perché, diciamocelo, come non essere curiosi di sentire un'opinione sull'ultimo album del king del rap? E per concludere, l'algoritmo non si dimentica di me e mi lancia nel mondo di Pulp Podcast, con Fedez e Mr. Marra che chiacchierano di tutto, tranne forse di calcio o cinema, ma chi può dirlo, giusto? Un mix esplosivo che mi fa davvero interrogare su quanto l'algoritmo abbia afferrato la mia vera essenza.

Quindi tra una riflessione sul mio team di fantacalcio e un salto in un podcast che non avrei mai cercato, l'algoritmo riesce a farmi scoprire qualcosa che non sapevo nemmeno di voler vedere. È quasi come se, tra un video e l’altro, mi stesse invitando a esplorare nuovi angoli del mio stesso interesse.

E qui sta il dilemma: da un lato, ci sentiamo "manipolati" dall’algoritmo; dall’altro, non possiamo negare che spesso ci azzecchi, rendendo la nostra esperienza più fluida e facendoci scoprire nuovi contenuti senza doverli cercare attivamente. Ma come funzionano davvero questi sistemi? Lo scopriremo in questo articolo insieme man mano.

La struttura tipica di un sistema di raccomandazione

Per capire come i sistemi di raccomandazione basati sui contenuti riescano a suggerirci esattamente ciò che ci interessa, dobbiamo analizzarne la struttura. Questi sistemi si basano su tre componenti principali:

1. Generazione dei candidati – Il primo passo è selezionare un insieme ristretto di elementi potenzialmente rilevanti per l’utente. Dato l’enorme numero di contenuti disponibili, il sistema filtra e crea un sottogruppo di opzioni che potrebbero essere di interesse, riducendo così la complessità della selezione.
2. Sistemi di punteggio – Una volta generato il set di candidati, ogni elemento deve essere valutato e classificato. Diversi modelli possono essere utilizzati per assegnare un punteggio a ciascun contenuto, basandosi su criteri come la rilevanza rispetto alle preferenze dell’utente, la popolarità o caratteristiche specifiche degli elementi.
3. Sistemi di ri-ordinamento (reranking) – Dopo l’assegnazione del punteggio, il sistema applica ulteriori filtri e regolazioni per affinare il ranking finale. Qui possono entrare in gioco fattori come il contesto d’uso, la varietà dei suggerimenti o eventuali vincoli personalizzati.

Queste componenti consentono ai sistemi di raccomandazione di affinare progressivamente le loro proposte, garantendo che i contenuti suggeriti non siano solo pertinenti, ma anche diversificati e contestualmente appropriati per ogni utente. Ma come fa un algoritmo a capire quali elementi suggerire?

Nel Content-Based Filtering, i sistemi analizzano le caratteristiche degli elementi stessi per individuare quelli più simili a ciò che l’utente ha già apprezzato. Se hai guardato una serie TV di genere thriller, è probabile che la piattaforma ti suggerisca altri contenuti simili, basandosi su parametri come il regista, il cast o la trama. Tuttavia, affinché il sistema funzioni in modo efficace, è necessario definire con precisione come rappresentare utenti e contenuti. Questo avviene attraverso modelli matematici che trasformano informazioni testuali e metadati in strutture interpretabili dagli algoritmi.

Un aspetto chiave è il calcolo della similarità tra gli elementi, che può essere determinato tramite metriche come la cosine similarity, la distanza euclidea o il dot product. Questi strumenti permettono di posizionare gli elementi in uno spazio vettoriale, dove la vicinanza tra due punti indica una maggiore somiglianza.

Nel corso dell’articolo, analizzeremo in dettaglio il funzionamento di questi algoritmi, esplorando i metodi di rappresentazione dei dati, le metriche di similarità e i vantaggi e svantaggi di questo approccio rispetto ad altre tecniche di raccomandazione come il Collaborative Filtering.

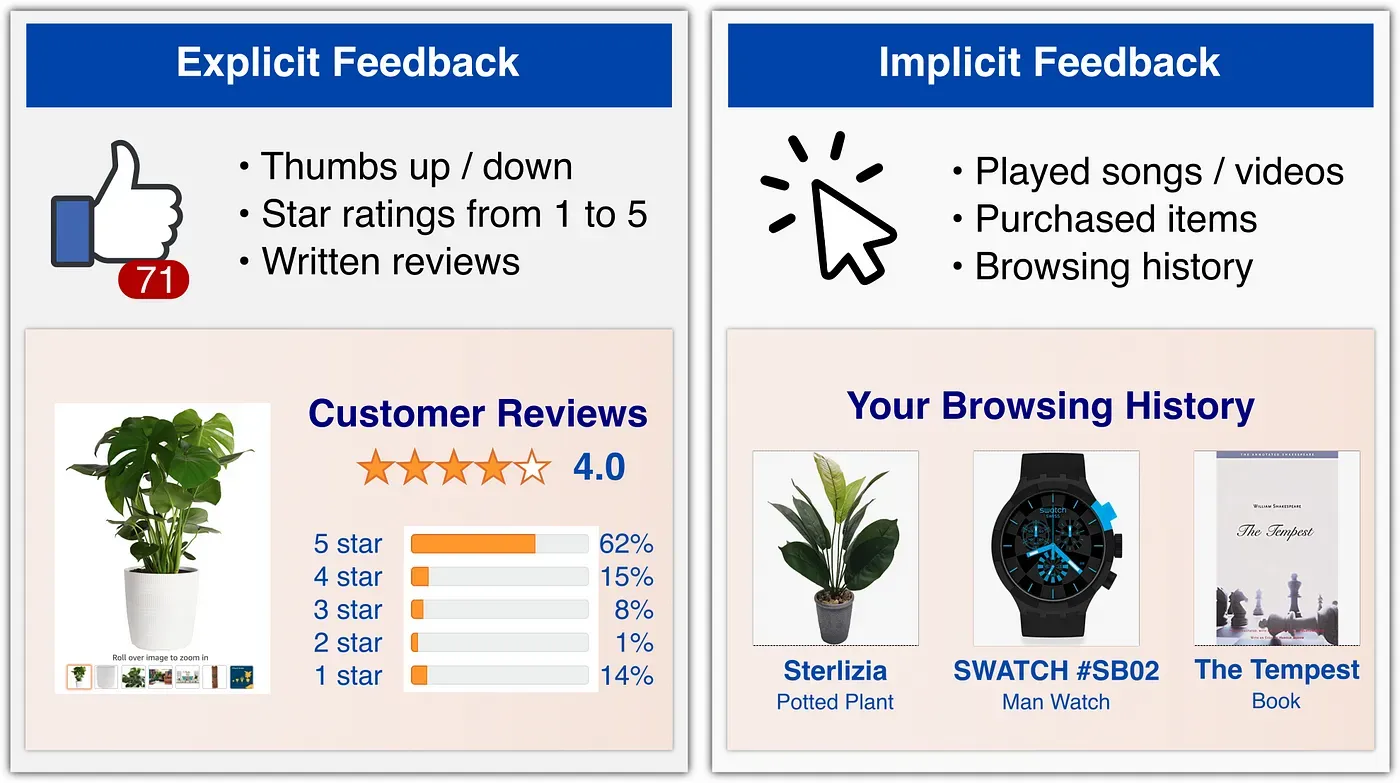
Feedback implicito vs esplicito

Nei sistemi di raccomandazione, la qualità delle previsioni dipende fortemente dai dati raccolti sugli utenti e sui loro comportamenti. La matrice di valutazione utente-elemento \( ruir_{ui} \) rappresenta una delle basi fondamentali per l’addestramento dei modelli di machine learning impiegati per generare suggerimenti personalizzati. Tuttavia, questa matrice è generalmente molto sparsa, poiché gli utenti interagiscono solo con una piccola frazione degli elementi disponibili su una piattaforma, e ancora meno frequentemente lasciano un feedback esplicito.

La raccolta del feedback è cruciale per il funzionamento di un sistema di raccomandazione, poiché rappresenta la cosiddetta "verità di base" (ground truth) su cui vengono addestrati i modelli predittivi.

Feedback esplicito

Il feedback esplicito è costituito da informazioni fornite direttamente dagli utenti, come valutazioni in stelle, recensioni scritte o reazioni (pollice in su/giù).

Questo tipo di feedback offre dati chiari e interpretabili, poiché riflette un giudizio diretto dell’utente sulla qualità dell’elemento valutato. Tuttavia, presenta alcune limitazioni:

• Bassa copertura: solo una piccola percentuale di utenti fornisce attivamente valutazioni, lasciando molti elementi privi di dati.
• Bias di auto-selezione: gli utenti tendono a recensire solo gli elementi che hanno forti opinioni, positive o negative, portando a una distribuzione distorta del feedback.
• Sovraccarico cognitivo: chiedere all’utente di valutare manualmente ogni interazione può ridurre il suo coinvolgimento con la piattaforma.

Nonostante questi limiti, il feedback esplicito è particolarmente utile in scenari in cui la precisione della raccomandazione è critica, come nel caso delle recensioni di prodotti o nella selezione di contenuti premium.

Feedback implicito

Il feedback implicito, invece, è raccolto passivamente attraverso le azioni dell’utente, come il tempo trascorso su un video, i clic su un articolo, gli acquisti effettuati o le canzoni ascoltate ripetutamente. Questo tipo di feedback ha il vantaggio di essere molto abbondante, permettendo di costruire modelli su dataset enormi. Tuttavia, presenta alcune sfide:

• Ambiguità dell'intenzione: il fatto che un utente guardi un film non significa necessariamente che gli sia piaciuto; potrebbe averlo lasciato in riproduzione senza attenzione o averlo abbandonato prima della fine.
• Dati rumorosi: alcuni comportamenti possono essere influenzati da fattori esterni, come l’acquisto di un regalo per qualcun altro, che non riflette necessariamente i gusti dell'utente.
• Necessità di tecniche avanzate: per estrarre informazioni utili dal feedback implicito, è necessario adottare modelli di apprendimento automatico più sofisticati, capaci di distinguere tra segnali rilevanti e rumore.

La matrice di valutazione utente-elemento

Una volta raccolti i dati di interazione, sia espliciti che impliciti, possiamo costruire la matrice di valutazione utente-elemento \( ruir_{ui} \), dove:

• Nel caso del feedback esplicito, ogni valore \( ruir_{ui} \) è un numero che rappresenta la valutazione data dall’utente \( uu \) all’elemento \( ii \), oppure un punto interrogativo “?” se l’utente non ha lasciato una valutazione.
• Nel caso del feedback implicito, i valori sono generalmente booleani o pesati in base all’intensità dell’interazione (es. numero di volte in cui un utente ha ascoltato una canzone).

Il problema principale di questa matrice è la sua elevata sparsità, cioè la presenza di molti valori mancanti dovuti alla scarsità di interazioni dirette tra utenti ed elementi. Per affrontare questa sfida, i sistemi di raccomandazione adottano diverse strategie, come:

• Interpolazione tramite metodi di Collaborative Filtering, che inferiscono valori mancanti basandosi su utenti o elementi simili;
• Approcci basati su modelli di apprendimento automatico, come le tecniche di Matrix Factorization (ad esempio, Singular Value Decomposition, SVD), che comprimono la matrice in una rappresentazione più compatta e gestibile;
• Uso di dati contestuali per arricchire il modello, incorporando informazioni aggiuntive come il momento della giornata, il dispositivo utilizzato o il contesto dell’interazione.

Il successo di un sistema di raccomandazione dipende dalla capacità di bilanciare questi due tipi di dati e di affrontare la sfida della sparsità della matrice \( ruir_{ui} \), garantendo suggerimenti pertinenti e personalizzati per ogni utente.

Content-Based vs. Collaborative Filtering

I sistemi di raccomandazione possono essere classificati in base al tipo di informazioni utilizzate per prevedere le preferenze degli utenti come Filtraggio Basato sui Contenuti (Content-Based) o Filtraggio Collaborativo (Collaborative Filtering).

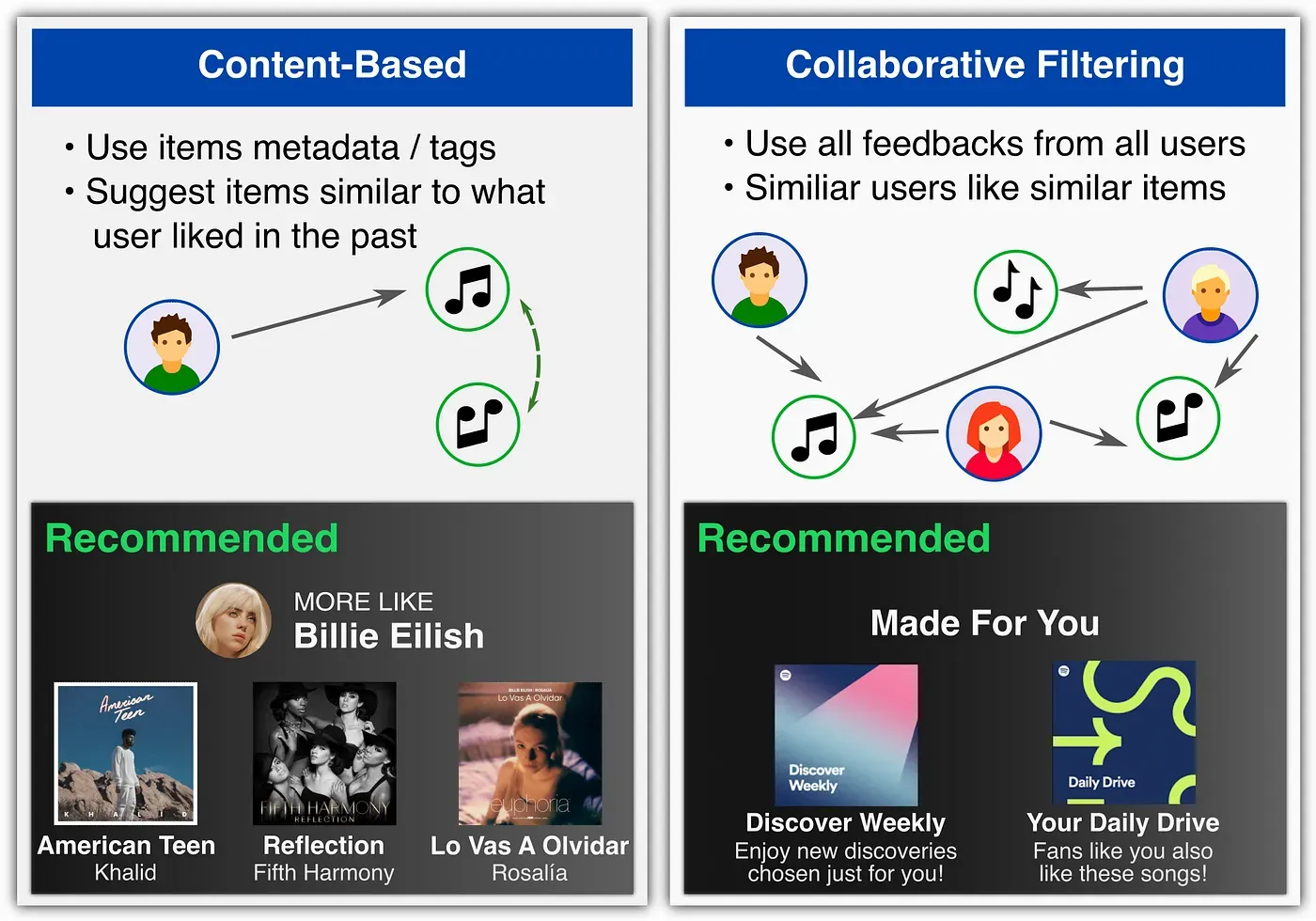
Il Filtraggio Basato sui Contenuti è una delle strategie più diffuse nei sistemi di raccomandazione e si fonda sull’idea che le preferenze di un utente possano essere dedotte analizzando le caratteristiche degli elementi che ha già apprezzato. Se un utente ha guardato numerosi film di fantascienza su una piattaforma di streaming, il sistema sarà in grado di suggerirgli altri titoli appartenenti allo stesso genere o con caratteristiche simili. Lo stesso principio si applica agli acquisti online, alle playlist musicali e persino agli articoli di giornale.

Vuoi leggere di più su questo argomento?

Recommender Systems: The Textbook

Charu C. Aggarwal

Questo libro copre in modo esaustivo la teoria dietro i sistemi di raccomandazione. Esposte diverse applicazioni, tra cui query log mining, social networking, raccomandazioni di notizie e pubblicità computazionale.

Compralo su Amazon

I metodi basati sui contenuti descrivono gli utenti e gli articoli tramite i loro metadati noti. Ogni articolo ii è rappresentato da un insieme di tag rilevanti—ad esempio, i film della piattaforma IMDb possono essere etichettati come “azione”, “commedia”, ecc. Ogni utente uu è rappresentato da un profilo utente, che può essere creato a partire da informazioni note sull'utente—ad esempio sesso e età—o dall'attività passata dell'utente.

Ad esempio, se sappiamo che l'utente \( uu \) ha acquistato un articolo \( ii \), possiamo raccomandare all'utente \( uu \) gli articoli disponibili con caratteristiche più simili a \( ii \).

Il vantaggio di questo approccio è che i metadati degli articoli sono noti in anticipo, quindi possiamo applicarlo anche in scenari di Cold-Start, dove un nuovo articolo o utente viene aggiunto alla piattaforma e non abbiamo interazioni utente-articolo per addestrare il nostro modello. Gli svantaggi sono che non utilizziamo l'intero insieme delle interazioni note utente-articolo (ogni utente è trattato indipendentemente) e che dobbiamo conoscere le informazioni sui metadati per ogni articolo e utente.

A seconda dell’algoritmo impiegato, il filtraggio basato sui contenuti può funzionare in modi diversi. Alcuni sistemi si basano sui metadati associati agli elementi, come il genere di un film, l’autore di un libro o le parole chiave che descrivono un articolo. Altri algoritmi, invece, analizzano direttamente il contenuto effettivo, utilizzando tecniche avanzate di elaborazione del linguaggio naturale per i testi o sistemi di riconoscimento delle immagini per le foto e i video. Indipendentemente dall’approccio adottato, l’obiettivo è sempre quello di individuare elementi con caratteristiche simili a quelli già apprezzati dall’utente, in modo da offrirgli suggerimenti pertinenti e personalizzati.

Questo metodo si contrappone al Filtraggio Collaborativo, un’altra tecnica ampiamente utilizzata nei sistemi di raccomandazione. Mentre il filtraggio basato sui contenuti si concentra esclusivamente sulle proprietà degli elementi, quello collaborativo analizza il comportamento di più utenti, raggruppandoli in base a preferenze simili. Un sistema collaborativo, ad esempio, potrebbe suggerire un film a un utente non perché appartiene a un genere che ha già apprezzato, ma perché è stato visto e valutato positivamente da altri utenti con gusti affini ai suoi.

I metodi di filtraggio collaborativo non utilizzano i metadati degli articoli o degli utenti, ma cercano invece di sfruttare i feedback o la cronologia delle attività di tutti gli utenti per prevedere la valutazione di un utente su un determinato articolo, inferendo le interdipendenze tra utenti e articoli dalle attività osservate.
Per addestrare un modello di Machine Learning con questo approccio, tipicamente cerchiamo di raggruppare o fattorizzare la matrice delle valutazioni \( ruir_{ui} \) al fine di fare previsioni sulle coppie non osservate \(u, i\), cioè dove \(rui=“?”r_{ui} = “?”\). Il vantaggio di questo approccio è che viene utilizzato l'intero insieme delle interazioni utente-articolo (cioè la matrice \( ruir_{ui} \)), il che consente generalmente di ottenere una maggiore precisione rispetto ai modelli basati sui contenuti. Lo svantaggio di questo approccio è che richiede alcune interazioni utente prima che il modello possa essere addestrato.

Per superare i limiti dei singoli approcci, molte piattaforme adottano oggi sistemi di raccomandazione ibridi, che combinano il filtraggio basato sui contenuti con quello collaborativo. Un esempio celebre è Netflix, che nel 2009 ha organizzato il Netflix Prize, una competizione per migliorare il proprio sistema di raccomandazione attraverso l’uso di modelli ibridi. Questi sistemi sfruttano le caratteristiche degli elementi per offrire suggerimenti mirati, ma al tempo stesso analizzano le preferenze di altri utenti con gusti simili per ampliare la gamma di raccomandazioni e rendere l’esperienza di scoperta più varia e interessante.

Il filtraggio basato sui contenuti continua a essere uno degli strumenti più efficaci per personalizzare l’esperienza degli utenti nelle piattaforme digitali. Utilizzato in ambiti che vanno dall’e-commerce ai social media, fino ai servizi di streaming, il suo impiego consente di ridurre il tempo di ricerca e aumentare l’engagement, offrendo suggerimenti su misura per ogni utente. Sebbene presenti alcune limitazioni, la sua capacità di analizzare e comprendere le preferenze individuali lo rende un pilastro fondamentale dei moderni sistemi di raccomandazione.

Metriche di similarità

Nei sistemi di raccomandazione basati sui contenuti, una delle tecniche più utilizzate per misurare la similarità tra gli elementi è la similarità del coseno. Questo metodo si basa sul calcolo dell’angolo tra due vettori in uno spazio vettoriale multidimensionale, piuttosto che sulla loro distanza euclidea. L’idea fondamentale è che due elementi saranno considerati simili se i loro vettori hanno una direzione simile, indipendentemente dalla loro lunghezza.

Immaginiamo di avere due romanzi rappresentati come vettori in uno spazio in cui ogni dimensione corrisponde a un genere letterario. Se entrambi i romanzi appartengono ai generi fantasy e avventura, ma uno è più lungo dell’altro (ovvero ha più parole chiave associate), la loro distanza euclidea potrebbe risultare elevata, anche se condividono molte caratteristiche. La similarità del coseno, invece, si concentra esclusivamente sull’orientamento dei vettori, fornendo una misura più affidabile della loro somiglianza concettuale.

Matematicamente, la similarità del coseno tra due vettori \( x \) e \( y \) è definita dalla formula:

\( \text{Cosine Similarity} = \frac{x \cdot y}{|x| |y|} \)

dove:

• \( x \cdot y \) è il prodotto scalare tra i due vettori,
• \( |x| \) e \( |y| \) sono le norme (o lunghezze) dei vettori, calcolate come la radice quadrata della somma dei quadrati dei loro componenti.

Questa formula produce un valore compreso tra -1 e 1:

• 1 indica che i vettori sono perfettamente allineati e quindi rappresentano elementi identici o altamente simili.
• 0 significa che i vettori sono ortogonali, ossia non condividono alcuna caratteristica in comune.
• -1 suggerisce una correlazione negativa, che tuttavia nei sistemi di raccomandazione è meno comune, poiché le caratteristiche degli elementi sono solitamente rappresentate con valori non negativi.

Uno dei principali vantaggi della similarità del coseno è la sua efficacia negli spazi ad alta dimensionalità, come quelli tipici dei sistemi di raccomandazione, dove ogni elemento può essere descritto da centinaia o migliaia di caratteristiche. Poiché non dipende direttamente dalla grandezza dei vettori, è meno influenzata dalla presenza di elementi con più attributi rispetto ad altri, rendendola ideale per analizzare contenuti con lunghezze diverse, come documenti di testo, film con molteplici etichette di genere o prodotti con descrizioni dettagliate.

Un caso d’uso pratico della similarità del coseno si trova nei sistemi di raccomandazione di libri o film. Supponiamo che un utente abbia apprezzato un romanzo di fantascienza con elementi distopici e un altro romanzo con una forte componente tecnologica. Utilizzando la similarità del coseno, il sistema può identificare nuovi titoli che si trovano nello stesso spazio vettoriale, privilegiando quelli con un alto grado di correlazione rispetto a quelli con una semplice sovrapposizione parziale di generi. In definitiva, la similarità del coseno rappresenta uno strumento essenziale nei sistemi di filtraggio basato sui contenuti, permettendo di quantificare con precisione il grado di affinità tra gli elementi e migliorare l’accuratezza delle raccomandazioni offerte agli utenti.

Un'alternativa alla similarità del coseno per misurare la somiglianza tra elementi nei sistemi di raccomandazione è la distanza euclidea. Questo metodo si basa sulla distanza geometrica tra due punti in uno spazio vettoriale e misura quanto due elementi siano effettivamente "distanti" l'uno dall'altro.

La distanza euclidea tra due vettori \( x \) e \( y \) in uno spazio \( n \)-dimensionale è data dalla formula:

\( d(x, y) = \sqrt{\sum_{i=1}^{n} (x_i - y_i)^2} \)

dove:

• \( x_i \) e \( y_i \) sono i valori delle coordinate dei due vettori nelle \( n \) dimensioni,
• la somma dei quadrati delle differenze tra le coordinate viene calcolata per ogni dimensione,
• si estrae la radice quadrata del valore ottenuto per ottenere la distanza effettiva.

Questa formula riflette il concetto di distanza cartesiana nel piano o nello spazio tridimensionale, ma può essere applicata anche a spazi con un numero molto elevato di dimensioni, come avviene nei sistemi di raccomandazione.

Immaginiamo di avere due film rappresentati da vettori numerici, in cui ogni dimensione corrisponde a un genere cinematografico, come azione, dramma, commedia e così via. Se un film ha un punteggio alto in "azione" e "fantascienza", mentre un altro ha punteggi alti in "dramma" e "storico", la loro distanza euclidea sarà elevata, indicando una bassa somiglianza. Al contrario, due film con valori simili nelle stesse categorie avranno una distanza ridotta, suggerendo che siano più affini e quindi potenzialmente raccomandabili allo stesso tipo di utente.

Uno dei principali vantaggi della distanza euclidea è la sua intuitività: maggiore è la distanza tra due punti, minore è la loro somiglianza. Questo approccio funziona bene quando le caratteristiche degli elementi sono distribuite in modo uniforme e hanno scale di valori comparabili. Tuttavia, presenta anche alcune limitazioni:

• Sensibilità alla scala dei dati
  Se le variabili hanno scale molto diverse, la distanza euclidea può risultare distorta. Ad esempio, se un sistema di raccomandazione include variabili come il numero di pagine di un libro (che può variare da 100 a 1000) e il numero di generi a cui appartiene (tipicamente da 1 a 5), la componente "numero di pagine" avrà un peso sproporzionato sulla distanza calcolata. Per mitigare questo problema, è spesso necessario normalizzare i dati.
• Problemi in spazi ad alta dimensionalità
  In spazi con molte dimensioni (ad esempio, quando gli elementi sono descritti da centinaia di caratteristiche), la distanza euclidea tende a perdere efficacia. Questo fenomeno è noto come "maledizione della dimensionalità": a mano a mano che il numero di dimensioni aumenta, la distanza tra i punti diventa meno discriminante, rendendo più difficile distinguere tra elementi simili e dissimili.
• Maggiore influenza della magnitudine dei vettori
  A differenza della similarità del coseno, la distanza euclidea è sensibile alla grandezza dei vettori. Se un elemento ha più caratteristiche rispetto a un altro (ad esempio, un film con molte parole chiave associate rispetto a un altro con poche), la distanza euclidea potrebbe risultare elevata, anche se le proporzioni tra le caratteristiche fossero simili.

Quando usare la distanza euclidea rispetto alla similarità del coseno

La Distanza euclidea è più adatta quando i dati hanno una scala uniforme e le caratteristiche degli elementi non sono distribuite su spazi troppo complessi. È particolarmente utile nei modelli basati su clustering, come il k-means, dove i punti vicini vengono raggruppati insieme. Invece la Similarità del coseno è preferibile quando le caratteristiche degli elementi hanno scale diverse o quando si lavora con dati sparsi e ad alta dimensionalità, come nei sistemi di raccomandazione testuali o basati su parole chiave.

In conclusione, mentre la distanza euclidea fornisce una misura intuitiva della dissimilarità tra elementi, la similarità del coseno è spesso una scelta più robusta nei contesti di raccomandazione, dove la direzione del vettore è più importante della sua magnitudine. Tuttavia, in alcuni scenari, come il clustering o il confronto tra elementi con caratteristiche omogenee, la distanza euclidea può ancora rappresentare un'opzione efficace per identificare somiglianze tra gli elementi.

Il prodotto scalare è una delle tecniche fondamentali per misurare la similarità tra vettori nei sistemi di raccomandazione basati sui contenuti. Esso fornisce un'indicazione del grado di correlazione tra due vettori nello stesso spazio, prendendo in considerazione sia l'orientamento sia la magnitudine dei vettori stessi.

Formalmente, il prodotto scalare tra due vettori \( d \) e \( q \) è definito come:

\( \text{Dot Product} = \sum_{i=1}^{n} d_i \cdot q_i \)

dove:

• \( d_i \) e \( q_i \) rappresentano i valori delle coordinate dei vettori \( d \) e \( q \) lungo la \( i \)-esima dimensione dello spazio vettoriale,
• \( n \) è il numero totale delle dimensioni (ovvero il numero di caratteristiche con cui gli elementi sono rappresentati).

Il prodotto scalare può anche essere espresso come:

\( d \cdot q = |d| |q| \cos \theta \)

dove:

• \( |d| \) e \( |q| \) sono le norme euclidee dei vettori (cioè le loro lunghezze),
• \( \theta \) è l'angolo tra i due vettori,
• \( \cos \theta \) è il valore del coseno dell'angolo tra i due vettori.

Questa formula mostra come il prodotto scalare sia strettamente legato alla similarità del coseno: mentre la similarità del coseno normalizza il valore rispetto alla lunghezza dei vettori, il prodotto scalare mantiene la dipendenza dalla loro magnitudine. Il prodotto scalare è utile quando la magnitudine dei vettori è significativa e si desidera dare più peso a elementi con caratteristiche dominanti. È spesso utilizzato nei modelli di deep learning per raccomandazioni, come quelli basati su reti neurali. Se si vuole una misura che consideri solo l'orientamento dei vettori e non la loro grandezza, la similarità del coseno è una scelta più appropriata. Quando si desidera una misura di distanza che consideri direttamente le differenze assolute tra elementi, la distanza euclidea può essere preferibile.

Nei sistemi di raccomandazione basati sui contenuti, il prodotto scalare viene utilizzato per confrontare la rappresentazione vettoriale di elementi come film, libri o prodotti. Se un elemento è descritto da un vettore che contiene informazioni su generi, autori o caratteristiche tecniche, allora il prodotto scalare tra due vettori ci dirà quanto questi elementi siano "allineati" nelle loro caratteristiche. Ad esempio, consideriamo due film rappresentati da vettori che contengono informazioni sui loro generi, espressi con valori numerici. Se un film ha un alto valore nelle dimensioni "fantascienza" e "azione", e un altro film ha valori simili nelle stesse categorie, il loro prodotto scalare sarà elevato, indicando una forte somiglianza. Al contrario, se i due vettori hanno valori significativi in dimensioni completamente diverse (ad esempio, un film d'azione e un documentario storico), il loro prodotto scalare sarà basso o addirittura nullo, segnalando una bassa affinità.

Uno dei principali vantaggi del prodotto scalare è la sua semplicità computazionale: rispetto ad altre misure di similarità, come la distanza euclidea o la similarità del coseno, il calcolo del prodotto scalare richiede solo una moltiplicazione e una somma per ogni dimensione dello spazio vettoriale.

Questo lo rende particolarmente efficiente nei sistemi di raccomandazione in tempo reale.Tuttavia, il prodotto scalare presenta alcune limitazioni. Infatti,
a differenza della similarità del coseno, che si concentra solo sull'angolo tra i vettori, il prodotto scalare dipende anche dalla loro lunghezza. Questo significa che elementi con valori molto alti in tutte le dimensioni tenderanno a ottenere prodotti scalari maggiori, anche se il loro orientamento non è perfettamente allineato con altri elementi.

Inoltre, poiché il valore del prodotto scalare può variare sensibilmente in base alla lunghezza dei vettori, non fornisce sempre una misura coerente della similarità tra elementi con caratteristiche di scala diversa. Ad esempio, se due film sono descritti da un numero molto diverso di parole chiave, il prodotto scalare potrebbe sovrastimare la loro somiglianza. Per mitigare questo effetto, il prodotto scalare viene spesso combinato con la normalizzazione della lunghezza dei vettori, trasformandolo di fatto nella similarità del coseno.

Il prodotto scalare è spesso utilizzato nei modelli di embedding per sistemi di raccomandazione, come quelli basati su Word2Vec o matrix factorization. Ad esempio, nei sistemi di raccomandazione di film o musica, i contenuti e gli utenti possono essere rappresentati come vettori nello stesso spazio, e il prodotto scalare tra il vettore di un utente e il vettore di un film può essere utilizzato per stimare il grado di preferenza dell'utente per quel film.In conclusione, il prodotto scalare è una tecnica potente per quantificare la somiglianza tra elementi nei sistemi di raccomandazione, ma deve essere utilizzato con attenzione per evitare distorsioni dovute alla differenza di scala tra i vettori.

Queste metriche di similarità sono sensibili al modo in cui i vettori vengono ponderati, poiché assegnare pesi differenti alle caratteristiche può alterare significativamente il risultato delle funzioni di punteggio. Ad esempio, nei sistemi di raccomandazione basati sui contenuti, l'importanza attribuita a ciascun attributo di un elemento (come il genere di un film o l'autore di un libro) può influenzare le raccomandazioni finali. Un peso maggiore assegnato a certe caratteristiche può enfatizzare la loro rilevanza rispetto ad altre, mentre una ponderazione uniforme può portare a risultati più bilanciati ma meno mirati.

Oltre alla similarità del coseno, alla distanza euclidea e al prodotto scalare, esistono altre metriche utilizzate per determinare la similarità tra vettori, ciascuna con applicazioni e vantaggi specifici. Una di queste è il coefficiente di correlazione di Pearson, che misura la relazione lineare tra due variabili e può essere utile nei sistemi di raccomandazione basati su feedback esplicito, come valutazioni a stelle o punteggi numerici assegnati dagli utenti. La correlazione di Pearson varia tra -1 e 1, dove valori positivi indicano una relazione diretta tra i vettori e valori negativi suggeriscono una relazione inversa.

Un'altra metrica comunemente usata è la similarità di Jaccard, particolarmente utile per dati binari o categoriali. Questa misura confronta due insiemi, calcolando il rapporto tra l'intersezione e l'unione degli elementi presenti nei due vettori. È spesso applicata nei sistemi di raccomandazione basati su feedback implicito, come l'acquisto di prodotti o la visualizzazione di film, poiché consente di misurare la sovrapposizione tra gli interessi degli utenti.

Un'altra alternativa è l'indice di Dice, strettamente correlato alla similarità di Jaccard, ma con una formula leggermente diversa che enfatizza maggiormente l'intersezione tra gli insiemi. L'indice di Dice è particolarmente utile quando si desidera attribuire più peso agli elementi in comune rispetto alla dimensione totale dell'unione.

La scelta della metrica di similarità più adatta dipende dal tipo di dati disponibili e dall'obiettivo specifico del sistema di raccomandazione. In alcuni casi, combinare più metriche o adottare approcci ibridi può migliorare la qualità delle raccomandazioni, fornendo risultati più precisi e pertinenti per l'utente finale.

Matrix Factorization nei Sistemi di Raccomandazione

Uno dei metodi più efficaci e utilizzati nei sistemi di raccomandazione è la Matrix Factorization, una tecnica che consente di decomporre la matrice utente-elemento in rappresentazioni più compatte e informative. Questo approccio è particolarmente utile per affrontare il problema della sparsità dei dati, ovvero la presenza di molteplici valori mancanti nelle interazioni tra utenti ed elementi.

Nei sistemi di raccomandazione, possiamo rappresentare le preferenze degli utenti attraverso una matrice delle valutazioni, in cui ogni riga corrisponde a un utente e ogni colonna a un elemento (film, libro, prodotto, ecc.). Il problema principale è che la maggior parte delle celle della matrice rimane vuota, poiché ogni utente interagisce solo con una piccola frazione degli elementi disponibili. La Matrix Factorization affronta questa difficoltà riducendo la dimensionalità della matrice e trovando rappresentazioni latenti per utenti ed elementi.

Matematicamente, il metodo più comune di Matrix Factorization è la Decomposizione ai Minimi Quadrati Alternati (ALS - Alternating Least Squares) o l'uso di tecniche come Singular Value Decomposition (SVD). L'obiettivo è fattorizzare la matrice utente-elemento RR in due matrici più piccole:

\( R \approx U \cdot V^T \)

dove:

• \( U \) è la matrice dei fattori latenti degli utenti, che rappresenta ogni utente in uno spazio vettoriale compatto.
• \( V \) è la matrice dei fattori latenti degli elementi, che rappresenta ogni elemento nello stesso spazio latente.

Il prodotto tra \( U \) e \( V^T \) permette di ricostruire le valutazioni mancanti nella matrice originale, fornendo così una stima per gli elementi non ancora valutati dagli utenti.

Uno degli aspetti più potenti della Matrix Factorization è la sua capacità di scoprire relazioni latenti tra utenti ed elementi, anche quando non ci sono interazioni dirette tra di essi. Ad esempio, se un utente ha guardato diversi film di fantascienza ma non ha ancora visto "Interstellar", il modello potrebbe inferire che quel film sia una buona raccomandazione basandosi sui pattern appresi dagli altri utenti con preferenze simili.

La Matrix Factorization è particolarmente efficace nei sistemi di raccomandazione basati sul filtraggio collaborativo, in cui si cercano schemi nelle interazioni utente-elemento piuttosto che nelle caratteristiche esplicite degli elementi stessi (come avviene nel filtraggio basato sui contenuti). Tuttavia, questo approccio può essere migliorato ulteriormente combinandolo con informazioni aggiuntive, come metadati sugli utenti o sugli elementi, dando vita a modelli ibridi in grado di offrire raccomandazioni ancora più precise e personalizzate.

L'importanza della Matrix Factorization nei sistemi di raccomandazione è stata evidenziata dal Netflix Prize, la famosa competizione del 2009 in cui team di ricercatori hanno migliorato il sistema di suggerimenti di Netflix utilizzando proprio tecniche di Matrix Factorization. Da allora, questo approccio è stato ampiamente adottato in molte piattaforme digitali, dagli e-commerce ai servizi di streaming, dimostrandosi un metodo efficace per migliorare la qualità delle raccomandazioni personalizzate.

Applicazione in Python

Dopo aver esplorato i principi teorici dei sistemi di raccomandazione, in questo capitolo ci concentreremo sulle loro applicazioni pratiche utilizzando Python. Vedremo come implementare un sistema di raccomandazione sfruttando librerie come scikit-learn per il calcolo della similarità tra elementi, e pandas per la gestione dei dati. Attraverso esempi concreti, costruiremo un modello in grado di suggerire elementi basandosi sulle caratteristiche testuali degli oggetti, dimostrando la potenza di questo approccio in scenari reali.

import numpy as np 
import pandas as pd

df1 = pd.read_csv("/content/tmdb_5000_credits.csv")
df2 = pd.read_csv("/content/tmdb_5000_movies.csv")

df1.columns = ['id','tittle','cast','crew']
df2= df2.merge(df1,on='id')

TMDB 5000 Movie Dataset

Metadata on ~5,000 movies from TMDb

Kaggle

Il primo dataset contiene le seguenti variabili:

• movie_id – Un identificatore univoco per ogni film.
• cast – Il nome degli attori principali e di supporto.
• crew – Il nome del regista, montatore, compositore, sceneggiatore, ecc.

Il secondo dataset contiene le seguenti variabili:

• budget – Il budget con cui è stato realizzato il film.
• genre – Il genere del film, ad esempio Azione, Commedia, Thriller, ecc.
• homepage – Un link alla homepage del film.
• id – Questo è in realtà lo stesso movie_id presente nel primo dataset.
• keywords – Le parole chiave o i tag associati al film.
• original_language – La lingua in cui è stato realizzato il film.
• original_title – Il titolo del film prima della traduzione o dell'adattamento.
• overview – Una breve descrizione del film.
• popularity – Un valore numerico che indica la popolarità del film.
• production_companies – La casa di produzione del film.
• production_countries – Il paese in cui è stato prodotto il film.
• release_date – La data di uscita del film.
• revenue – Il guadagno mondiale generato dal film.
• runtime – La durata del film in minuti.
• status – "Released" (Rilasciato) o "Rumored" (Rumoreggiato).
• tagline – Lo slogan del film.
• title – Il titolo del film.
• vote_average – Il voto medio ricevuto dal film.
• vote_count – Il numero totale di voti ricevuti.

Uniamo i due dataset sulla colonna "id".

Abbiamo osservato che nel nostro dataset sono state utilizzate oltre 20.000 parole per descrivere 4.800 film. Con al matrice TF-IDF a disposizione, possiamo ora calcolare un indice di similarità. Non esiste una risposta univoca su quale sia la migliore, poiché diversi metodi funzionano meglio in contesti diversi. Spesso è utile sperimentare con più metriche per determinare quale sia la più adatta. Per il nostro caso, utilizzeremo la similarità del coseno per calcolare un valore numerico che esprima la somiglianza tra due film.

Poiché abbiamo utilizzato il vettorizzatore TF-IDF, il calcolo del prodotto scalare ci fornirà direttamente il valore della similarità del coseno. Per questo motivo, utilizzeremo la funzione linear_kernel() di scikit-learn invece di cosine_similarity(), poiché è più veloce ed efficiente. Definiremo una funzione che prende come input il titolo di un film e restituisce una lista dei 10 film più simili. Per fare ciò, innanzitutto, abbiamo bisogno di una mappatura inversa tra i titoli dei film e gli indici del DataFrame. In altre parole, dobbiamo creare un meccanismo che ci permetta di identificare l'indice di un film nel nostro DataFrame di metadati, dato il suo titolo.

Adesso possiamo definire la nostra funzione di raccomandazione. Per prima cosa, otteniamo l'indice del film dato il suo titolo. Successivamente, otteniamo la lista dei punteggi di similarità del coseno per quel particolare film rispetto a tutti gli altri film, e la convertono in una lista di tuple dove il primo elemento è la sua posizione e il secondo è il punteggio di similarità. Poi ordiniamo questa lista di tuple in base ai punteggi di similarità, cioè al secondo elemento. Dopodiché prendiamo i primi 10 elementi di questa lista, ignorando il primo elemento in quanto si riferisce al film stesso (il film più simile a un particolare film è lo stesso film). Infine, restituiamo i titoli corrispondenti agli indici degli elementi principali.

# Importa TfidfVectorizer da scikit-learn
from sklearn.feature_extraction.text import TfidfVectorizer

# Definisce un oggetto TF-IDF Vectorizer. Rimuove tutte le stopwords in inglese come 'the', 'a'
tfidf = TfidfVectorizer(stop_words='english')

# Sostituisce i valori NaN con una stringa vuota
df2['overview'] = df2['overview'].fillna('')

# Costruisce la matrice TF-IDF richiesta adattando e trasformando i dati
tfidf_matrix = tfidf.fit_transform(df2['overview'])

# Restituisce la forma della matrice TF-IDF
tfidf_matrix.shape #(4803, 20978)

# Importa linear_kernel
from sklearn.metrics.pairwise import linear_kernel

# Calcola la matrice di similarità del coseno
cosine_sim = linear_kernel(tfidf_matrix, tfidf_matrix)

# Costruisce una mappa inversa di indici e titoli dei film
indices = pd.Series(df2.index, index=df2['title']).drop_duplicates()

# Funzione che prende in input il titolo di un film e restituisce i film più simili
def get_recommendations(title, cosine_sim=cosine_sim):
    # Ottiene l'indice del film che corrisponde al titolo
    idx = indices[title]

    # Ottiene i punteggi di similarità tra tutti i film e il film selezionato
    sim_scores = list(enumerate(cosine_sim[idx]))

    # Ordina i film in base ai punteggi di similarità
    sim_scores = sorted(sim_scores, key=lambda x: x[1], reverse=True)

    # Ottiene i punteggi dei 10 film più simili
    sim_scores = sim_scores[1:11]

    # Ottiene gli indici dei film
    movie_indices = [i[0] for i in sim_scores]

    # Restituisce i 10 film più simili
    return df2['title'].iloc[movie_indices]

get_recommendations('The Dark Knight Rises')

               title
65	The Dark Knight
299	Batman Forever
428	Batman Returns
1359	Batman
3854	Batman: The Dark Knight Returns, Part 2
119	Batman Begins
2507	Slow Burn
9	Batman v Superman: Dawn of Justice
1181	JFK
210	Batman & Robin

dtype: object

get_recommendations('The Avengers')

          title
7	Avengers: Age of Ultron
3144	Plastic
1715	Timecop
4124	This Thing of Ours
3311	Thank You for Smoking
3033	The Corruptor
588	Wall Street: Money Never Sleeps
2136	Team America: World Police
1468	The Fountain
1286	Snowpiercer

Mentre il nostro sistema di raccomandazione ha fatto un buon lavoro nel trovare film con descrizioni di trama simili, la qualità delle raccomandazioni non è eccezionale. Ad esempio, "The Dark Knight Rises" restituisce tutti i film di Batman, mentre è più probabile che le persone che hanno apprezzato quel film siano più inclini a visionare altri film di Christopher Nolan. Questo è un aspetto che l'attuale sistema non riesce a catturare.

È evidente che la qualità del nostro sistema di raccomandazione migliorerebbe utilizzando metadati migliori. Questo è esattamente ciò che faremo in questa sezione. Creeremo un sistema di raccomandazione basato sui seguenti metadati: i 3 principali attori, il regista, i generi correlati e le parole chiave della trama del film.

Dai dati relativi al cast, alla troupe e alle parole chiave, dobbiamo estrarre i tre attori più importanti, il regista e le parole chiave associate a ciascun film. Al momento, i nostri dati sono rappresentati come liste "stringificate", quindi dobbiamo convertirli in una struttura sicura e utilizzabile.

# Converte le caratteristiche in formato stringa nei corrispondenti oggetti Python
from ast import literal_eval

features = ['cast', 'crew', 'keywords', 'genres']
for feature in features:
    df2[feature] = df2[feature].apply(literal_eval)


# Estrae il nome del regista dalla caratteristica 'crew'. Se non è presente, restituisce NaN
def get_director(x):
    for i in x:
        if i['job'] == 'Director':
            return i['name']
    return np.nan


# Restituisce i primi 3 elementi della lista o l'intera lista se ha meno di 3 elementi
def get_list(x):
    if isinstance(x, list):
        names = [i['name'] for i in x]
        # Controlla se ci sono più di 3 elementi. Se sì, restituisce solo i primi tre, altrimenti l'intera lista.
        if len(names) > 3:
            names = names[:3]
        return names

    # Restituisce una lista vuota in caso di dati mancanti o non validi
    return []


# Definisce nuove caratteristiche per il regista, il cast, i generi e le parole chiave in un formato adeguato
df2['director'] = df2['crew'].apply(get_director)

features = ['cast', 'keywords', 'genres']
for feature in features:
    df2[feature] = df2[feature].apply(get_list)

# Stampa le nuove caratteristiche per i primi 3 film
df2[['title', 'cast', 'director', 'keywords', 'genres']].head(3)

Il passo successivo sarà convertire i nomi e le istanze delle parole chiave in minuscolo e rimuovere tutti gli spazi tra di esse. Questo viene fatto per evitare che il nostro vettorizzatore consideri "Johnny" di "Johnny Depp" e "Johnny Galecki" come lo stesso termine.

# Funzione per convertire tutte le stringhe in minuscolo e rimuovere gli spazi nei nomi
def clean_data(x):
    if isinstance(x, list):
        return [str.lower(i.replace(" ", "")) for i in x]
    else:
        # Controlla se il regista esiste. Se no, restituisce una stringa vuota
        if isinstance(x, str):
            return str.lower(x.replace(" ", ""))
        else:
            return ''

# Applica la funzione clean_data alle caratteristiche selezionate
features = ['cast', 'keywords', 'director', 'genres']

for feature in features:
    df2[feature] = df2[feature].apply(clean_data)

Adesso possiamo creare la nostra "metadata soup", che è una stringa che contiene tutti i metadati che vogliamo fornire al nostro vettorizzatore (ossia attori, regista e parole chiave).

# Funzione per creare la "soup" di metadati combinando parole chiave, cast, regista e generi
def create_soup(x):
    return ' '.join(x['keywords']) + ' ' + ' '.join(x['cast']) + ' ' + x['director'] + ' ' + ' '.join(x['genres'])

df2['soup'] = df2.apply(create_soup, axis=1)

# Importa CountVectorizer e crea la matrice di conteggio
from sklearn.feature_extraction.text import CountVectorizer

count = CountVectorizer(stop_words='english')
count_matrix = count.fit_transform(df2['soup'])

# Calcola la matrice di similarità del coseno basata sulla count_matrix
from sklearn.metrics.pairwise import cosine_similarity

cosine_sim2 = cosine_similarity(count_matrix, count_matrix)

# Reimposta l'indice del DataFrame principale e costruisce la mappatura inversa come prima
df2 = df2.reset_index()
indices = pd.Series(df2.index, index=df2['title'])


get_recommendations('The Dark Knight Rises', cosine_sim2)

	    title
65	The Dark Knight
119	Batman Begins
4638	Amidst the Devil's Wings
1196	The Prestige
3073	Romeo Is Bleeding
3326	Black November
1503	Takers
1986	Faster
303	Catwoman
747	Gangster Squad

get_recommendations('The Godfather', cosine_sim2)
	    title
867	The Godfather: Part III
2731	The Godfather: Part II
4638	Amidst the Devil's Wings
2649	The Son of No One
1525	Apocalypse Now
1018	The Cotton Club
1170	The Talented Mr. Ripley
1209	The Rainmaker
1394	Donnie Brasco
1850	Scarface

Vediamo come il nostro sistema di raccomandazione sia riuscito a catturare più informazioni grazie all’uso di metadati aggiuntivi, fornendo (probabilmente) raccomandazioni migliori. È più probabile che i fan della Marvel o della DC Comics apprezzino i film della stessa casa di produzione.

Per questo motivo, possiamo arricchire ulteriormente il nostro modello aggiungendo la casa di produzione tra le caratteristiche utilizzate. Inoltre, possiamo aumentare il peso del regista ripetendo questa informazione più volte nella "metadata soup".

Vantaggi e svantaggi del Filtraggio Basato sui Contenuti

Come abbiamo visto nel corso di questo articolo, i sistemi di raccomandazione basati sui contenuti (CBRS) offrono una serie di vantaggi significativi, ma presentano anche alcune limitazioni.

Un grande vantaggio del filtraggio basato sui contenuti è la sua capacità di gestire il problema del cold-start. Mentre i sistemi collaborativi hanno difficoltà con nuovi utenti o nuovi elementi, il CBRS può facilmente consigliare nuovi articoli, libri, o film, basandosi sulle caratteristiche o metadati descrittivi degli elementi, anche senza alcuna interazione precedente. Inoltre, questi sistemi tendono a offrire un maggiore livello di trasparenza, poiché gli utenti possono comprendere più facilmente perché un certo contenuto è stato suggerito. Se un utente riceve una raccomandazione di un film basato sul genere o sul regista, può decidere più consapevolmente se seguirla o meno.

Tuttavia, ci sono anche degli svantaggi. Infatti, il sistema può consigliare solo ciò che è simile a ciò che l'utente ha già apprezzato, ma senza esplorare aspetti più sottili o nuovi gusti. Questo porta al problema dell'iperspecializzazione, dove il sistema rischia di "ingabbiare" l'utente in un ciclo di raccomandazioni che non porta a scoperte inaspettate. Inoltre, se le caratteristiche non sono abbastanza dettagliate o se non riflettono correttamente le vere preferenze dell'utente, le raccomandazioni possono risultare poco accurate o addirittura deludenti.

Riassumendo, abbiamo esplorato in profondità come funzionano i sistemi di raccomandazione basati sui contenut, passando dai modelli di previsione dell’interazione utente-elemento, alle diverse metriche di similarità come il coseno e il prodotto scalare, fino a discutere della matrix factorization come tecnica avanzata per migliorare la personalizzazione delle raccomandazioni. Abbiamo esaminato come questi sistemi utilizzano le caratteristiche degli elementi per consigliare contenuti simili a quelli che l'utente ha apprezzato in passato, ma anche le sfide legate alla loro natura, come la difficoltà di suggerire contenuti nuovi e sorprendenti.

Non possiamo dimenticare i vantaggi, come la gestione efficace dei nuovi contenuti e la trasparenza, ma anche i limiti del CBRS, come l'iperspecializzazione e la difficoltà di captare sfumature più complesse nei gusti degli utenti.

E ora, arrivati alla fine, ci chiediamo: siamo davvero schiavi dell'algoritmo? O ci aiuta a scoprire contenuti che altrimenti non avremmo mai trovato? La risposta, come spesso accade, sta nel mezzo. Ora che sappiamo come funzionano questi sistemi, abbiamo il potere di scegliere se farci "manipolare" o meno. Possiamo decidere di affidarci alle raccomandazioni, fidarci dell'algoritmo e lasciarci sorprendere, o possiamo scegliere di cercare qualcosa di nuovo, fuori dai suggerimenti preimpostati. In ogni caso, la consapevolezza è la chiave: ora sappiamo che dietro ogni raccomandazione c'è una logica complessa che analizza il nostro comportamento e le nostre preferenze. In fondo, siamo noi a fare la scelta finale—e questo è un grande passo verso la libertà nel mondo digitale.