Introduzione agli autoencoder

In questo articolo tratteremo gli autoencoder - particolari architetture di reti neurali che imparano a ricostruire i dati in input attraverso una compressione di questi ultimi.

Trovano molte applicazioni in contesti specifici, come l'identificazione delle anomalie, il clustering e la ricostruzione di feature.

Vuoi leggere di più su questo argomento?

Machine Learning Engineering

Andriy Burkov

Questo è IL libro di IA applicata più completo in circolazione. È pieno di best practice e modelli di progettazione per la creazione di soluzioni di apprendimento automatico affidabili e scalabili.

Compralo su Amazon

Cosa è un autoencoder?

Un autoencoder è una particolare architettura di rete neurale progettata per apprendere una rappresentazione compressa dei dati di input, chiamata codifica.

L'obiettivo principale è quello di ricostruire l'input originale a partire da questa rappresentazione compressa. Per immaginarlo in modo semplice, pensiamo ad una macchina fotografica: l'autoencoder è come se scattasse una foto in cui cerca di catturare solo i dettagli essenziali di un'immagine (la compressione) per poi ricostruirla fedelmente. Durante questo processo, l'autoencoder "impara" quali sono le caratteristiche fondamentali dei dati.

Quando l'autoencoder lavora, trasforma i dati di input in una rappresentazione più compatta definitia spazio latente. Lo spazio latente è un insieme di variabili latenti, cioè variabili che non possiamo osservare direttamente, ma che rappresentano aspetti importanti dei dati originali. Ad esempio, se l'input fosse un'immagine di un volto, le variabili latenti potrebbero includere informazioni come l'orientamento del viso, l'illuminazione o la presenza di occhiali.

Durante l'addestramento, l'autoencoder impara a identificare quali caratteristiche sono davvero utili per ricostruire i dati originali. In altre parole, riduce il superfluo e trattiene solo ciò che è essenziale.

Perché gli autoencoder sono utili?

Gli autoencoder sono strumenti estremamente versatili nell'ambito dell'intelligenza artificiale e trovano applicazione in diversi campi, come:

• Compressione dei dati: riducono la quantità di informazioni necessarie per rappresentare i dati, utile per archiviare immagini o video in meno spazio.
• Denoising: rimuovono il rumore dalle immagini, migliorandone la qualità. Ad esempio, possono ripulire una foto scattata con poca luce.
• Rilevamento delle anomalie: possono identificare dati anomali, come transazioni fraudolente in un sistema finanziario.
• Riconoscimento facciale: estraggono caratteristiche essenziali dai volti, semplificando il confronto tra immagini.

Queste applicazioni sono solo alcune tra le più rilevanti, e una volta compresi, gli autoencoder possono essere utilizzati per casi specifici in base al contesto di applicazione.

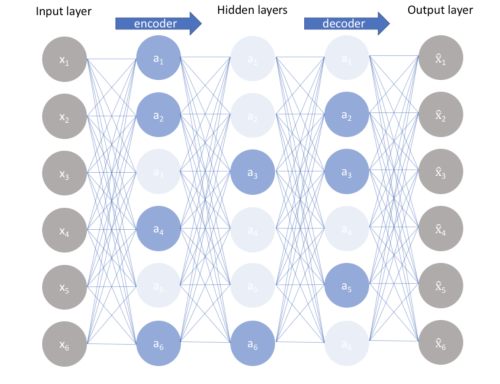
Anatomia di un autoencoder

Un autoencoder è sempre composto da due parti principali: un encoder (codificatore) che trasforma i dati di input in una rappresentazione compatta e un decoder che utilizza questa rappresentazione per ricostruire l'input originale. Tuttavia, non tutti i modelli encoder-decoder sono autoencoder.

Cos'è un modello encoder-decoder?

Un modello encoder-decoder è un'architettura flessibile usata in molte applicazioni di deep learning. In questo tipo di modello, l'encoder estrae le caratteristiche essenziali dall'input, mentre il decoder genera un output a partire da queste caratteristiche. A differenza degli autoencoder, l'output non è necessariamente una copia dell'input.

Per esempio nella traduzione automatica (modelli sequence-to-sequence, seq2seq), l'encoder trasforma una frase in una lingua (ad esempio, l'italiano) in una rappresentazione latente, che il decoder utilizza per generare la traduzione in un'altra lingua (ad esempio, l'inglese).

Nei modelli di segmentazione delle immagini come U-Net, l'encoder estrae caratteristiche dell'immagine (ad esempio, bordi o texture), mentre il decoder le utilizza per costruire maschere di segmentazione che identificano oggetti specifici nell'immagine. In questi casi, i modelli encoder-decoder sono addestrati in modalità supervisionata, utilizzando dati etichettati. Nel caso della segmentazione delle immagini, il modello apprende confrontando le sue previsioni (maschere generate) con le maschere fornite dagli esperti.

Gli autoencoder: un caso speciale

Gli autoencoder, invece, sono un caso particolare di modelli encoder-decoder e vengono utilizzati per ricostruire l'input originale. La loro particolarità è che funzionano in modalità non supervisionata: non richiedono dati etichettati per l'addestramento.

L'obiettivo dell'autoencoder è scoprire le caratteristiche nascoste nei dati. Tuttavia, ciò che rende un autoencoder unico è la sua forma di apprendimento, che viene spesso definita auto-supervisionata. Anche se non richiede etichette esterne, ha un obiettivo chiaro con cui misurare la bontà della sua previsione: l'input originale. Questo permette all'autoencoder di valutare quanto bene sta ricostruendo i dati, cosa che tipicamente non succede in uno scenario non supervisionato.

Come funzionano gli autoencoder?

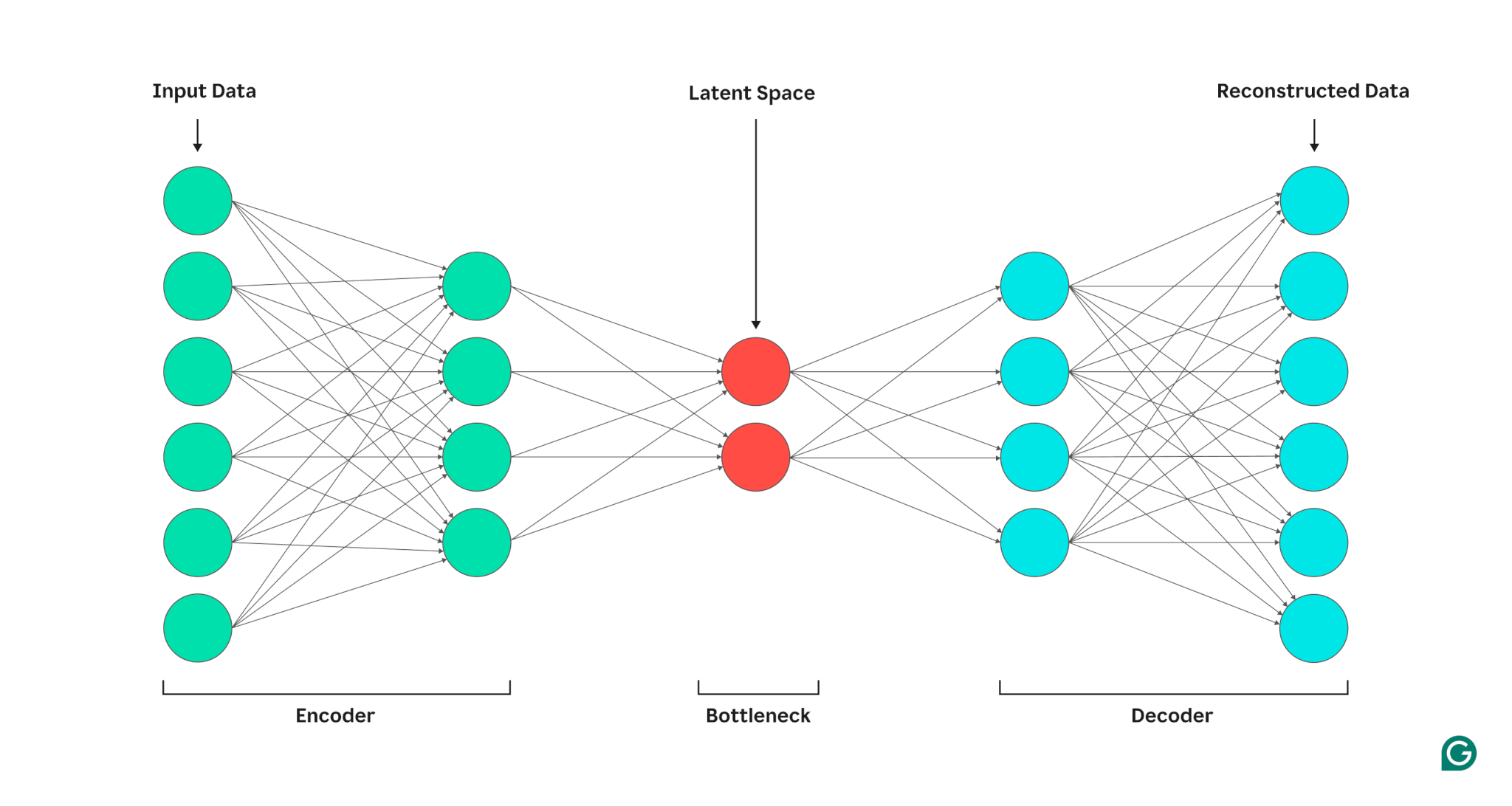
Gli autoencoder sono reti neurali progettate per comprimere e poi ricostruire i dati di input. Per farlo, passano l’input attraverso una struttura chiamata collo di bottiglia (bottleneck), che forza il modello a estrarre solo le informazioni essenziali. Questo processo consente agli autoencoder di identificare pattern nascosti nei dati e di comprimere grandi quantità di informazioni in rappresentazioni compatte.

Struttura di base di un autoencoder

Tutti gli autoencoder seguono una struttura fondamentale composta da tre parti principali:

• Encoder: è responsabile della compressione dei dati. Quando un dato di input passa attraverso gli strati dell’encoder, viene progressivamente ridotto in dimensionalità. Ad esempio se hai un’immagine con milioni di pixel, l’encoder riduce questa immagine a un insieme molto più piccolo di numeri che rappresentano solo le informazioni più rilevanti. Questo processo è simile a comprimere un file ZIP: elimini il superfluo per conservare solo l’essenza del contenuto.
• Collo di bottiglia: questa è la parte più compatta dell’architettura. Il codice generato rappresenta una versione ridotta e astratta dell’input originale. È come riassumere un libro di 1000 pagine in un paragrafo: il codice deve contenere abbastanza dettagli per permettere al decoder di ricostruire l’intera storia.
• Decoder: il decoder fa l’inverso dell’encoder: prende il codice compresso e lo “decomprime” per ricostruire il dato originale. Ad esempio se l’input originale era un’immagine, il decoder prova a ricreare la stessa immagine, pixel per pixel, a partire dal codice.

Caratteristiche uniche degli autoencoder

Una delle principali forze degli autoencoder rispetto ad altre tecniche di riduzione della dimensionalità, come la PCA (Analisi delle Componenti Principali), è la loro capacità di catturare relazioni non lineari nei dati. Questo è possibile grazie all’uso di funzioni di attivazione non lineari, come la funzione sigmoidea o ReLU.

Gli autoencoder possono essere personalizzati per diversi tipi di dati e applicazioni:

• Dati sequenziali: attraverso RNN o LSTM, adatti per testo o serie temporali.
• Immagini: mediante CNN, ottimali per foto e video.
• Dati complessi: con architetture ibride o transformer.

Fattori chiave nella progettazione di un autoencoder

La dimensione del collo di bottiglia (detto anche codice) determina quanto è compressa la rappresentazione dei dati. Un codice troppo grande potrebbe portare a una ricostruzione quasi perfetta, ma rischia di perdere il valore della compressione. Un codice troppo piccolo, invece, potrebbe non contenere abbastanza informazioni per una buona ricostruzione.

Inoltre, aumentare la profondità dell’autoencoder permette al modello di catturare pattern più complessi, ma potrebbe rallentare il processo di addestramento. Successivamente, gli strati dell’encoder riducono progressivamente il numero di nodi, raggiungendo il minimo nel collo di bottiglia. Successivamente, gli strati del decoder aumentano il numero di nodi per riportare il dato alla forma originale. Per concludere, la scelta della funzione di perdita dipende dal tipo di dato e dall’applicazione.  

Gli autoencoder incompleti

Gli autoencoder incompleti rappresentano una delle varianti più semplici e fondamentali degli autoencoder, progettati principalmente per la riduzione della dimensionalità. La caratteristica distintiva di questa architettura è la presenza di un collo di bottiglia fisso, con livelli nascosti che contengono meno nodi rispetto ai livelli di input e output.

Come funzionano gli autoencoder incompleti?

La compressione tramite il collo di bottiglia agisce come una restrizione sulla capacità della rete, costringendo il modello a comprimere l'input in una rappresentazione a bassa dimensionalità.

Tale compressione obbliga l’encoder a conservare solo le caratteristiche essenziali dell’input, quelle necessarie per una ricostruzione accurata. Senza limitare la capacità del collo di bottiglia, la rete potrebbe facilmente adattarsi eccessivamente ai dati di addestramento, apprendendo la semplice funzione identità: \( \text{output} = \text{input} \). Questo accade perché il modello, senza vincoli, può copiare i dati di input direttamente nell’output, senza mai catturare pattern significativi o strutture utili.

Questo tipo di autoencoder sono particolarmente efficaci per comprimere dati ad alta dimensionalità in una rappresentazione più compatta, utile per applicazioni come l’estrazione di caratteristiche o la visualizzazione in spazi ridotti. Nonostante i loro vantaggi, gli autoencoder incompleti presentano diverse limitazioni che ne riducono l’applicabilità in scenari complessi. Anche con un collo di bottiglia, se il modello ha un encoder e decoder composto da molteplici strati e nodi, può comunque apprendere la funzione identità, rendendo il modello inutile per applicazioni pratiche. La capacità fissa del collo di bottiglia rende questa architettura poco flessibile: potrebbe non adattarsi bene a dati complessi o di natura diversa, limitandone l’uso in applicazioni avanzate come la generazione di dati o la segmentazione di immagini.

Quando utilizzare gli autoencoder incompleti?

Gli autoencoder incompleti sono particolarmente utili in scenari in cui:

• L’obiettivo principale è la riduzione della dimensionalità.
• I dati sono relativamente semplici e non richiedono la modellazione di correlazioni non lineari molto complesse.
• Si desidera esplorare o visualizzare i dati in uno spazio latente compresso.

Autoencoder regolarizzati

Gli autoencoder regolarizzati rappresentano un’evoluzione rispetto agli autoencoder incompleti, progettati per superare i limiti di flessibilità e capacità di generalizzazione di questi ultimi. La chiave del loro funzionamento è l’introduzione di tecniche di regolarizzazione: aggiustamenti che modificano o limitano il modo in cui viene calcolato l’errore di ricostruzione durante l’addestramento. L'obiettivo non è soltanto ridurre il rischio di overfitting, ma anche garantire che il modello apprenda caratteristiche utili e ben strutturate dal dataset. 

Come funzionano gli autoencoder regolarizzati?

La regolarizzazione aggiunge un termine o un vincolo all’obiettivo di ottimizzazione dell'autoencoder (spesso espresso attraverso la funzione di perdita). Questo termine aggiuntivo guida il modello nell’apprendimento di pattern significativi, scoraggiando soluzioni banali come copiare semplicemente i dati di input. Alcune delle tecniche di regolarizzazione più comuni sono: 

• Autoencoder sparsi: i quali utilizzano un termine di regolarizzazione che forza solo alcuni neuroni a essere attivi contemporaneamente nello spazio latente, in modo che quest'ultimo diventa più interpretabile, favorendo una rappresentazione compatta ed essenziale dei dati. 
• Autoencoder di denoising: introducono rumore intenzionale ai dati di input e addestrano il modello a ricostruire l’input originale privo di rumore. Migliorando cosi la robustezza ai dati rumorosi e maggiore capacità di generalizzazione. 
• Autoencoder variazionali: impongono una distribuzione probabilistica (di solito gaussiana) sullo spazio latente, costringendo le rappresentazioni apprese a seguire una struttura statistica cosi alimentare la possibilità di generare nuovi dati simili all’input originale.  

Autoencoder sparsi

Sono una variante degli autoencoder che introducono un vincolo di scarsità sui nodi della rete neurale. Questo approccio consente di apprendere rappresentazioni significative anche con reti che hanno una maggiore capacità (ossia un numero elevato di nodi e strati), senza rischiare il sovradattamento. 

In un autoencoder standard incompleto, il collo di bottiglia delle informazioni viene creato riducendo il numero di nodi negli strati nascosti. Al contrario, negli autoencoder sparsi viene limitato il numero di neuroni attivati contemporaneamente per ogni osservazione. 

Ogni neurone che supera una soglia di attivazione specifica (ad esempio, un livello medio di attivazione desiderato) è penalizzato tramite un termine di regolarizzazione aggiunto alla funzione di perdita. Questo vincolo di scarsità forza la rete a rappresentare i dati in maniera efficace e attivare neuroni specifici solo quando le caratteristiche rappresentate da quei nodi sono presenti nei dati di input.

Divergenza di Kullback-Leibler

La divergenza di Kullback-Leibler è una misura di dissimilarità tra due distribuzioni di probabilità. Quando viene applicata agli autoencoder sparsi, la KL-divergence consente di imporre un vincolo di scarsità sui neuroni, penalizzando le attivazioni che si discostano da una distribuzione target desiderata.

Data una distribuzione target \( p \) (la scarsità desiderata) e una distribuzione effettiva \( q \) (la distribuzione dei valori di attivazione), la divergenza di KL è calcolata come:

\[KL(p \| q) = \sum_{i} p(i) \log \frac{p(i)}{q(i)}\]

 Dove: 

- \( p(i) \) è la probabilità desiderata di attivazione per il nodo \( i \). 

- \( q(i) \) è la probabilità effettiva di attivazione per il nodo \( i \). 

- La funzione logaritmica penalizza proporzionalmente le differenze tra \( p(i) \) e \( q(i) \). 

Negli SAE (sparse autoencoders), la divergenza di KL viene utilizzata come termine di regolarizzazione durante l'addestramento. Il processo avviene come segue:

• Distribuzione target: Ogni neurone nascosto ha una scarsità desiderata \( \rho \), che rappresenta il valore medio di attivazione previsto. Ad esempio, se \( \rho = 0.05 \), il neurone dovrebbe essere attivo solo nel 5% delle osservazioni. 
• Distribuzione effettiva: Durante l'addestramento, viene calcolata la media delle attivazioni effettive \( \hat{\rho} \) dei neuroni nascosti per un batch di dati. 
• Penalità di scarsità: Viene aggiunto un termine alla funzione di perdita che penalizza la rete per ogni neurone la cui \( \hat{\rho} \) si discosta da \( \rho \). La penalità di scarsità è proporzionale alla KL-divergence tra \( \rho \) e \( \hat{\rho} \):

\[Penalità = \sum_{j} \big[ \rho \log \frac{\rho}{\hat{\rho}_j} + (1 - \rho) \log \frac{1 - \rho}{1 - \hat{\rho}_j} \big]\]

Dove \( j \) è l'indice del nodo nascosto. 

Benefici della KL-divergence nei SAE

La divergenza di KL consente di regolare con precisione il livello di attivazione desiderato nei neuroni, adattandolo alla complessità dei dati. Garantendo che solo pochi neuroni si attivino contemporaneamente, i SAE favoriscono la scoperta di caratteristiche latenti utili e sparse. Limitando l'attivazione dei neuroni, la rete è meno incline a memorizzare i dettagli specifici dei dati di addestramento, migliorando la generalizzazione. 

La divergenza di KL è ampiamente utilizzata anche negli autoencoder variazionali (Variational Autoencoders (VAE)), ma con uno scopo diverso. Infatti, nei VAE, la KL-divergence misura la differenza tra la distribuzione appresa dallo spazio latente (ad esempio, una distribuzione gaussiana parametrizzata) e una distribuzione target (spesso una distribuzione normale standard). Questo vincolo guida il VAE a generare uno spazio latente ben organizzato e interpretabile. 

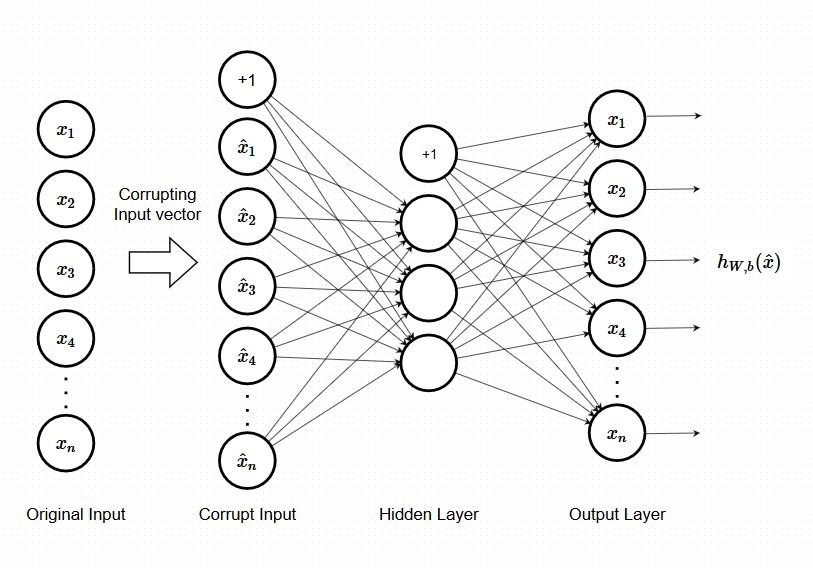
Autoencoder di denoising

Gli Autoencoder di denoising (DAE) sono una variante degli autoencoder progettata per apprendere a ripristinare dati corrotti eliminando il rumore aggiunto agli input. La loro capacità di ridurre il rumore li rende ideali per attività di pre-elaborazione e per costruire rappresentazioni latenti robuste.

Come funzionano i DAE

Durante l'addestramento, i dati di input vengono deliberatamente modificati aggiungendo rumore (ad esempio, rumore gaussiano, rumore salt-and-pepper, o mascherando alcune parti). L'obiettivo non è ricostruire i dati corrotti, ma recuperare la versione originale e priva di rumore. L'encoder riduce il dato corrotto a una rappresentazione compressa e robusta, il decoder ricostruisce il dato originale rimuovendo il rumore e l'errore di ricostruzione viene misurato confrontando l'output con la versione originale e non corrotta dei dati (la "ground truth").

La funzione di perdita valuta quanto l'output ricostruito si discosti dai dati originali. Un esempio comune di funzione di perdita è l'errore quadratico medio (MSE) tra i dati originali e quelli ricostruiti:

 \[Loss = \frac{1}{n} \sum_{i=1}^{n} (x_i - \hat{x}_i)^2\]

 Dove: 

- \( x_i \) sono i dati originali, 

- \( \hat{x}_i \) sono i dati ricostruiti, 

- \( n \) è il numero di osservazioni.

Vantaggi degli Autoencoder di Denoising

I DAE apprendono rappresentazioni che non dipendono da variazioni irrilevanti nei dati, rendendoli utili per lavorare con input rumorosi o parzialmente corrotti.

L'aggiunta di rumore aumenta implicitamente la variabilità dei dati di addestramento, agendo come una forma di regolarizzazione che riduce il rischio di memorizzare i dettagli specifici dei dati. I DAE sono utilizzati per "ripulire" dati rumorosi, come immagini e file audio, migliorando la qualità dei dati per ulteriori analisi. I principi del denoising sono stati adottati in architetture di generazione avanzate, come Stable Diffusion, per generare immagini di alta qualità a partire da input rumorosi.

Autoencoder variazionali

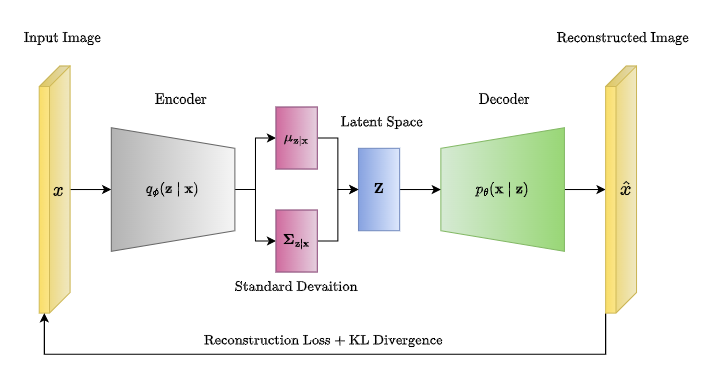
Gli autoencoder variazionali (VAE) rappresentano una sofisticata evoluzione degli autoencoder, progettati non solo per comprimere i dati, ma anche per generare nuovi campioni basati sulle distribuzioni apprese dai dati di addestramento. Questo li rende particolarmente potenti come modelli generativi probabilistici.

A differenza degli autoencoder standard che codificano l'input in un unico vettore discreto, i VAE modellano lo spazio latente come una distribuzione probabilistica continua. Lo spazio latente è rappresentato da due vettori: 

• Media (\( \mu \)):** rappresenta il centro della distribuzione latente. 
• Deviazione standard (\( \sigma \)):** rappresenta la variabilità attorno alla media.

I VAE non mappano un input in un singolo punto dello spazio latente, ma in una distribuzione, consentendo una generazione più varia di dati. Una volta addestrato, un VAE può campionare nuovi punti dallo spazio latente utilizzando una distribuzione normale standard. Grazie alla distribuzione probabilistica appresa, i nuovi campioni generati sono coerenti con la distribuzione originale dei dati di addestramento.

Funzione di perdita nei VAE

La funzione di perdita (loss) nei VAE combina due componenti: 

Errore di ricostruzione (\( \mathcal{L}_{rec} \)):

• Misura quanto bene il decoder ricostruisce l'input originale dai vettori latenti.
• Solitamente basata sull'errore quadratico medio (MSE) o sulla perdita cross-entropy. 

\[\mathcal{L}_{rec} = \| x - \hat{x} \|^2\]

Regolarizzazione tramite Divergenza di KL (\( \mathcal{L}_{KL} \)): 

• Penalizza la differenza tra la distribuzione latente appresa (\( q(z|x) \)) e una distribuzione prior definita (\( p(z) \)), tipicamente una normale standard (\( \mathcal{N}(0, I) \)). 
• Garantisce che i campioni generati dallo spazio latente siano coerenti con i dati originali. 

 \[\mathcal{L}_{KL} = D_{KL}(q(z|x) \, || \, p(z))\]

 La funzione di perdita complessiva è data da:

 \[\mathcal{L} = \mathcal{L}_{rec} + \beta \mathcal{L}_{KL}\]

Un elemento chiave dei VAE è il trucco di riparametrizzazione, che permette di campionare dallo spazio latente in modo differenziabile per consentire l'addestramento tramite retropropagazione.

 \[z = \mu + \epsilon \cdot \sigma\]

 Dove: 

• \( \epsilon \sim \mathcal{N}(0, 1) \) è un campione casuale dalla normale standard. 
• \( \mu \) e \( \sigma \) sono rispettivamente la media e la deviazione standard apprese dall'encoder. 

 Questo processo separa la parte stocastica (\( \epsilon \)) dalla parte appresa (\( \mu \) e \( \sigma \)), garantendo che il flusso del gradiente sia calcolabile.

Vantaggi dei VAE

I VAE possono generare nuovi dati coerenti con la distribuzione originale, utili per applicazioni come la generazione di immagini, segnali e testi. Poiché lo spazio latente è continuo, i VAE consentono di interpolare tra due punti nello spazio latente, generando transizioni fluide tra i dati. Varianti come i VAE Condizionali permettono di controllare le caratteristiche dei campioni generati fornendo input condizionali aggiuntivi.

Scrivere un autoencoder in Python 

Vedremo come scrivere un autoencoder in Python con Keras. Useremo il dataset di Credit Card Fraud da Kaggle. Raggiungibile e scaricabile al seguente link

Credit Card Fraud Detection

Anonymized credit card transactions labeled as fraudulent or genuine

Kaggle

Questo dataset contiene solo variabili di input numeriche che sono il risultato di una trasformazione PCA. Le caratteristiche V1, V2, … V28 sono i componenti principali ottenuti con PCA, le uniche caratteristiche che non sono state trasformate con PCA sono 'Time' e 'Amount'. La caratteristica 'Time' contiene i secondi trascorsi tra ogni transazione e la prima transazione nel set di dati. La caratteristica 'Amount' è l'Importo della transazione, questa caratteristica può essere utilizzata per l'apprendimento sensibile ai costi dipendente dall'esempio. La caratteristica 'Class' è la variabile di risposta e assume il valore 1 in caso di frode e 0 in caso contrario.

Utilizzeremo Keras e TensorFlow per implementare e addestrare l'autoencoder.

from keras.layers import Input, Dense
from keras.models import Model, Sequential
from keras import regularizers
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report, accuracy_score
from sklearn.manifold import TSNE
from sklearn import preprocessing
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import seaborn as sns
sns.set(style="whitegrid")
np.random.seed(203)

data = pd.read_csv("/content/drive/MyDrive/creditcard.csv")
data["Time"] = data["Time"].apply(lambda x : x / 3600 % 24)
data.head()

vc = data['Class'].value_counts().to_frame().reset_index()
vc['percent'] = vc["Class"].apply(lambda x : round(100*float(x) / len(data), 2))
vc = vc.rename(columns = {"index" : "Target", "Class" : "Count"})
vc

>>>
Target  Count   percent
0       284315  99.83
1       492     0.17

Il dataset, da come possiamo vedere, è fortemente sbilanciato ma l'approccio che useremo sarà capace di gestire questo tipo di problema. Nel nostro esempio useremo solo 1000 delle transazioni non fraudolenti.

non_fraud = data[data['Class'] == 0].sample(1000)
fraud = data[data['Class'] == 1]

df = pd.concat([non_fraud, fraud]).sample(frac=1).reset_index(drop=True)
X = df.drop(['Class'], axis=1).values
Y = df['Class'].values

Adesso visualizziamo le transazioni attraverso un particolare tipo di distribuzione chiamata T-SNE (t-Distributed Stochastic Neighbor Embedding). Questa è un tecnica di decomposizione del dataset la quale permette di ridurre la dimensionalità dei dati e produrre un dato numero di componenti con l'informazione massima.

Ogni punto indica una transazione, quelle non fraudolenti sono rappresentate dai punti verdi mentre quelle fraudolenti da quelli rossi. I due assi sono due componenti estratte dalla T-SNE.

import matplotlib.pyplot as plt
from sklearn.manifold import TSNE
import numpy as np

def tsne_plot(x1, y1, name="graph.png"):
    tsne = TSNE(n_components=2, random_state=0)
    X_t = tsne.fit_transform(x1)

    plt.figure(figsize=(12, 8))
    plt.scatter(X_t[np.where(y1 == 0), 0], X_t[np.where(y1 == 0), 1], marker='o', color='g', linewidth=1, alpha=0.8, label='Non Fraud')
    plt.scatter(X_t[np.where(y1 == 1), 0], X_t[np.where(y1 == 1), 1], marker='o', color='r', linewidth=1, alpha=0.8, label='Fraud')

    plt.legend(loc='best')
    plt.savefig(name)
    plt.show()

# Assuming X and Y are your data and labels
tsne_plot(X, Y, "original.png")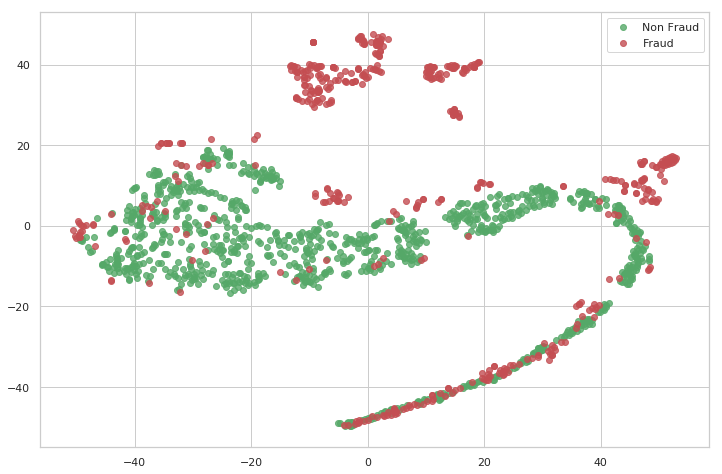

Dal grafico si evince come numerose transazioni non fraudolenti siano incredibilmente vicine alle altre, quindi questo renderà difficoltoso la loro corretta classificazione per il modello.

A questo punto sfruttiamo un modello autoencoder al quale mostreremo esclusivamente i casi non fraudolenti. Il modello cercherà di apprendere la migliore rappresentazione possibile dei casi non fraudolenti. Lo stesso modello verrà utilizzato per generare le rappresentazioni dei casi fraudolenti, e ci aspettiamo che queste siano diverse da quelle dei casi non fraudolenti.

Creiamo una rete con uno strato di input e uno strato di output aventi dimensioni identiche, cioè la stessa forma dei casi non fraudolenti.

## input layer
input_layer = Input(shape=(X.shape[1],))

## encoding part
encoded = Dense(100, activation='tanh', activity_regularizer=regularizers.l1(10e-5))(input_layer)
encoded = Dense(50, activation='relu')(encoded)

## decoding part
decoded = Dense(50, activation='tanh')(encoded)
decoded = Dense(100, activation='tanh')(decoded)

## output layer
output_layer = Dense(X.shape[1], activation='relu')(decoded)

autoencoder = Model(input_layer, output_layer)
autoencoder.compile(optimizer="adadelta", loss="mse")

#min max scaling
x = data.drop(["Class"], axis=1)
y = data["Class"].values

x_scale = preprocessing.MinMaxScaler().fit_transform(x.values)
x_norm, x_fraud = x_scale[y == 0], x_scale[y == 1]

La bellezza di questo approccio risiede nel fatto che non abbiamo bisogno di un numero elevato di campioni per apprendere buone rappresentazioni. Utilizzeremo solo 2000 righe di casi non fraudolenti per addestrare l'autoencoder. Inoltre, non è necessario eseguire il modello per un numero elevato di epoche.

La scelta di piccoli campioni dal dataset originale si basa sull'intuizione che le caratteristiche di una classe (non fraudolenta) differiranno da quelle dell'altra (fraudolenta). Per distinguere queste caratteristiche, è sufficiente mostrare agli autoencoder solo una classe di dati. Questo perché l'autoencoder cercherà di apprendere esclusivamente una classe e distinguerà automaticamente l'altra.

autoencoder.fit(x_norm[0:2000], x_norm[0:2000],
                batch_size = 256, epochs = 10,
                shuffle = True, validation_split = 0.20);
Epoch 1/10
7/7 ━━━━━━━━━━━━━━━━━━━━ 3s 33ms/step - loss: 0.9299 - val_loss: 0.8239
Epoch 2/10
7/7 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.9292 - val_loss: 0.8233
Epoch 3/10
7/7 ━━━━━━━━━━━━━━━━━━━━ 0s 7ms/step - loss: 0.9287 - val_loss: 0.8228
Epoch 4/10
7/7 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - loss: 0.9285 - val_loss: 0.8222
Epoch 5/10
7/7 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step - loss: 0.9277 - val_loss: 0.8216
Epoch 6/10
7/7 ━━━━━━━━━━━━━━━━━━━━ 0s 7ms/step - loss: 0.9269 - val_loss: 0.8210
Epoch 7/10
7/7 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.9264 - val_loss: 0.8204
Epoch 8/10
7/7 ━━━━━━━━━━━━━━━━━━━━ 0s 11ms/step - loss: 0.9253 - val_loss: 0.8198
Epoch 9/10
7/7 ━━━━━━━━━━━━━━━━━━━━ 0s 7ms/step - loss: 0.9246 - val_loss: 0.8192
Epoch 10/10
7/7 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.9243 - val_loss: 0.8186

Ora il modello è stato addestrato e siamo interessati a ottenere la rappresentazione latente dell'input appresa dal modello. Questa rappresentazione può essere ottenuta attraverso i pesi del modello addestrato.

hidden_representation = Sequential()
hidden_representation.add(autoencoder.layers[0])
hidden_representation.add(autoencoder.layers[1])
hidden_representation.add(autoencoder.layers[2])

norm_hid_rep = hidden_representation.predict(x_norm[:3000])
fraud_hid_rep = hidden_representation.predict(x_fraud)

94/94 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step
16/16 ━━━━━━━━━━━━━━━━━━━━ 0s 1ms/step

Adesso creiamo un dataset di addestramento utilizzando le rappresentazioni latenti ottenute e visualizzeremo i casi fraudolenti rispetto a quelli non fraudolenti.

rep_x = np.append(norm_hid_rep, fraud_hid_rep, axis = 0)
y_n = np.zeros(norm_hid_rep.shape[0])
y_f = np.ones(fraud_hid_rep.shape[0])
rep_y = np.append(y_n, y_f)
tsne_plot(rep_x, rep_y, "latent_representation.png")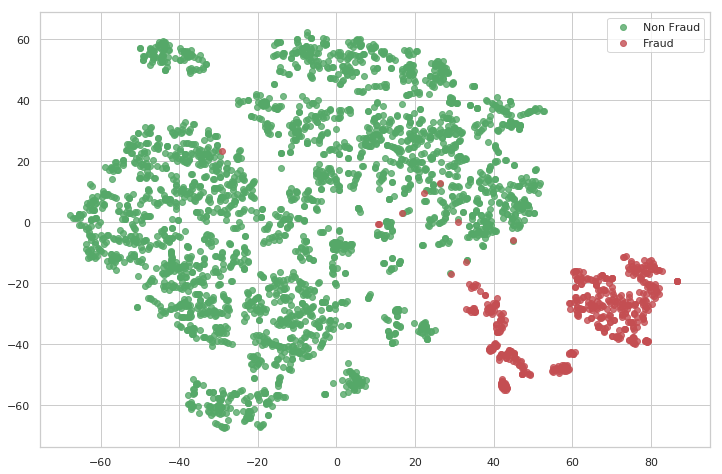

Da questo grafico possiamo osservare come le transazioni fraudolente e non fraudolente sono chiaramente visibili e linearmente separabili. Non è più necessario un modello complesso per classificare queste transazioni; anche i modelli più semplici possono essere utilizzati per effettuare previsioni.

train_x, val_x, train_y, val_y = train_test_split(rep_x, rep_y, test_size=0.25)
clf = LogisticRegression(solver="lbfgs").fit(train_x, train_y)
pred_y = clf.predict(val_x)

print ("")
print ("Classification Report: ")
print (classification_report(val_y, pred_y))

print ("")
print ("Accuracy Score: ", accuracy_score(val_y, pred_y))

Classification Report: 
              precision    recall  f1-score   support

         0.0       0.98      1.00      0.99       744
         1.0       1.00      0.86      0.93       129

    accuracy                           0.98       873
   macro avg       0.99      0.93      0.96       873
weighted avg       0.98      0.98      0.98       873


Accuracy Score:  0.97

Conclusione

Gli autoencoder rappresentano uno strumento affascinante e versatile. Da semplici rappresentazioni latenti a sofisticate applicazioni come la riduzione del rumore e la generazione di dati, queste reti neurali offrono soluzioni eleganti a problemi complessi. La varietà di approcci, dagli autoencoder incompleti a quelli variazionali, mostra come adattare queste architetture alle esigenze specifiche di un progetto.

Comprendere le differenze tra autoencoder ed encoder-decoder, così come le caratteristiche distintive di ogni tipologia, è fondamentale per sfruttarne al meglio il potenziale. Con il loro utilizzo crescente in ambiti come la rilevazione di anomalie, la compressione dei dati e la generazione di immagini, gli autoencoder continuano a rivoluzionare il modo in cui interpretiamo e utilizziamo i dati.

Esplorare questa tecnologia non solo permette di arricchire il nostro bagaglio tecnico, ma apre le porte a soluzioni innovative e a una comprensione più profonda dei dati che analizziamo.