Dati sintetici: superare le limitazioni dei dataset reali nel machine learning

Nel panorama contemporaneo della data science e del machine learning, i dati rappresentano la risorsa fondamentale per lo sviluppo di modelli predittivi e analisi accurate. Tuttavia, non sempre i dataset reali sono disponibili, completi o utilizzabili. Problemi come la scarsità dei dati, i bias intrinseci o le limitazioni legate alla privacy rendono spesso difficile l’accesso a dati di qualità. Qui entra in gioco il concetto di dati sintetici: dati artificiali generati con l’obiettivo di simulare le caratteristiche dei dati reali, preservando al contempo privacy e flessibilità.

L’obiettivo di questa guida è fornire una panoramica sulle tecniche per generare dati sintetici affidabili e utili. Questo include esplorare metodi probabilistici, tecniche di machine learning (ML) tradizionali e l’uso di modelli avanzati come i Large Language Models (LLM). Verranno presentati esempi concreti di utilizzo per creare dataset utili al training di modelli predittivi e altre analisi, garantendo che rispettino vincoli e caratteristiche tipiche dei dati reali.

Cosa sono i dati sintetici?

I dati sintetici sono informazioni artificialmente generate che imitano le caratteristiche dei dati reali. A differenza dei dati raccolti direttamente da osservazioni, esperimenti o sensori, i dati sintetici sono prodotti attraverso algoritmi, modelli matematici o tecniche avanzate di machine learning. Lo scopo principale è riprodurre la struttura statistica e le relazioni presenti in un dataset reale, pur essendo completamente inventati.

In molti ambiti applicativi, i dati raccolti possono essere insufficienti per sviluppare modelli robusti. Questo problema è particolarmente evidente in settori di nicchia, dove le osservazioni sono limitate, o in contesti emergenti, come le applicazioni industriali di IoT (internet of things). Generare dati sintetici permette di ampliare questi dataset, preservando le proprietà statistiche e strutturali fondamentali.

Questi dati non si limitano a essere copie anonime o modificate di dati esistenti, ma possono rappresentare scenari ipotetici o nuove combinazioni di variabili che non necessariamente si verificano nel dataset originale. Un esempio è la generazione di immagini sintetiche per addestrare modelli di riconoscimento visivo o di dati tabellari per simulare trend economici.

Cenni storici

La pratica di creare dati sintetici ha radici che risalgono agli anni '70 e '80, quando le simulazioni al computer cominciarono a guadagnare terreno nei settori scientifici e ingegneristici. Tecniche come il campionamento Monte Carlo erano già utilizzate per generare dati basati su distribuzioni matematiche.

Negli anni 2000, la crescente attenzione alla privacy e alle limitazioni legali nella condivisione di dati reali ha spinto verso la generazione di dati sintetici in ambiti come la sanità, la finanza e i servizi pubblici. Negli ultimi anni, l'avvento del machine learning ha trasformato profondamente il panorama. Metodi avanzati come i Large Language Models (LLM) consentono di creare dati altamente realistici con relazioni complesse e dettagliate.

Vantaggi e svantaggi di usare dati sintetici

Ecco una lista di motivazioni che ci fanno riflettere sul perché utilizzare metodi di generazione di dati sintetici.

1. Controllo totale: Poiché i dati sono generati artificialmente, è possibile modellarne con precisione le caratteristiche, come distribuzioni, correlazioni e outlier.
2. Scalabilità: Una volta progettato un generatore di dati sintetici, è possibile creare dataset di qualsiasi dimensione, adattandoli a specifiche esigenze di calcolo o analisi.
3. Riduzione dei bias: Quando progettati correttamente, i dati sintetici possono evitare i bias intrinseci che spesso affliggono i dati reali. Questo consente di testare modelli in condizioni più neutrali e controllate.
4. Costi ridotti: Generare dati sintetici è spesso più economico rispetto alla raccolta di dati reali, specialmente in settori che richiedono attrezzature sofisticate o risorse significative per l'acquisizione.
5. Preservare la privacy: I dati reali spesso contengono informazioni sensibili che non possono essere condivise senza rischi di violazione della privacy. Non essendo legati a individui reali, permettono di aggirare questo problema, pur mantenendo l’utilità analitica.
6. Superare la scarsità di dati: Raccogliere dati sufficienti è costoso o impraticabile come per addestrare un modello di visione artificiale su immagini di malattie rare. I dati sintetici consentono di ampliare i dataset senza costi aggiuntivi.
7. Facilitare la sperimentazione e lo sviluppo: I dati sintetici offrono un ambiente sicuro per testare algoritmi e modelli senza il rischio di esporre dati sensibili o di influenzare sistemi reali.
8. Creare scenari personalizzati: In alcune applicazioni, è necessario simulare eventi estremi o scenari improbabili difficili da osservare nel mondo reale. I dati sintetici consentono di costruire queste situazioni in modo controllato.

Nonostante i numerosi vantaggi, l'uso di dati sintetici comporta anche alcune sfide:

1. Validità dei dati sintetici: La qualità di un dataset sintetico dipende dalla capacità del modello generativo di catturare le caratteristiche del dominio di interesse. Se mal progettati, i dati sintetici possono introdurre errori o rappresentazioni distorte.
2. Accettazione delle normative: In alcuni settori, l'uso di dati sintetici potrebbe non essere pienamente accettato o normato, il che potrebbe limitare il loro utilizzo in contesti ufficiali.
3. Mantenimento delle relazioni complesse: Riprodurre relazioni intricate tra variabili, come quelle osservate nei sistemi biologici o finanziari, può essere particolarmente difficile.
4. Bias sintetici: Sebbene i dati sintetici possano ridurre i bias presenti nei dati reali, esiste il rischio di introdurre bias artificiali se il modello generativo è basato su presupposti non corretti.

È dunque fondamentale scegliere le tecniche appropriate e validare attentamente i risultati per garantire che questi dati siano utili e affidabili nel contesto specifico dell'applicazione.

Tecniche per la generazione di dati sintetici

La generazione di dati sintetici tramite tecniche probabilistiche si basa sull'uso di distribuzioni matematiche per simulare la variabilità osservata nei dataset reali. Questo approccio consente di modellare e creare dati che seguono una specifica distribuzione statistica, come quella normale, uniforme o binomiale. Questi metodi sono particolarmente utili per:

• Testare algoritmi in condizioni controllate
• Generare dataset per scenari dove i dati reali sono limitati o non disponibili
• Simulare relazioni tra variabili in base a modelli probabilistici definiti

Distribuzioni base

Le distribuzioni matematiche, come quella normale (Gaussiana), uniforme e Poisson, sono strumenti fondamentali per generare dati sintetici. Utilizzando le librerie Python come NumPy, è possibile creare dataset simulati che rappresentano scenari specifici.

Esempio: Generazione di un dataset con distribuzione normale

import numpy as np
import matplotlib.pyplot as plt

# Generazione di dati con distribuzione normale
mu, sigma = 0, 1  # Media e deviazione standard
data_normal = np.random.normal(mu, sigma, 1000)

# Visualizzazione
plt.hist(data_normal, bins=30, alpha=0.7, color='blue', edgecolor='black')
plt.title('Distribuzione Normale')
plt.xlabel('Valore')
plt.ylabel('Frequenza')
plt.show()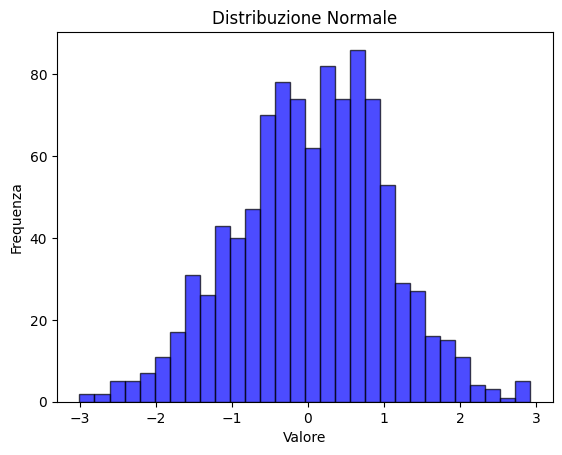

Campionamento Monte Carlo

Il campionamento Monte Carlo è una tecnica per generare dati simulando distribuzioni più complesse o definite da funzioni arbitrariamente complesse. È ideale per situazioni dove le distribuzioni semplici non sono sufficienti.

Esempio: Approssimazione di un'integrale usando Monte Carlo

import numpy as np
import matplotlib.pyplot as plt

# Parametri della distribuzione reale (tempi di attesa)
real_mu = 10  # Media
real_sigma = 2  # Deviazione standard
n_real_samples = 10000  # Numero di dati reali (campioni)

# Generazione dei dati reali (distribuzione osservata)
real_data = np.random.normal(real_mu, real_sigma, n_real_samples)

# Monte Carlo: campioni progressivi per approssimare la distribuzione reale
n_monte_carlo_samples = 500  # Numero massimo di campioni Monte Carlo
monte_carlo_data = np.random.normal(real_mu, real_sigma, n_monte_carlo_samples)

# Creazione di un grafico per confrontare distribuzione reale e simulazione Monte Carlo
plt.figure(figsize=(12, 6))

# Distribuzione reale
plt.hist(real_data, bins=30, alpha=0.5, color='blue', label='Distribuzione Reale', density=True)

# Distribuzione Monte Carlo
plt.hist(monte_carlo_data, bins=30, alpha=0.5, color='orange', label='Monte Carlo', density=True)

plt.title("Confronto tra Distribuzione Reale e Simulazione Monte Carlo")
plt.xlabel("Tempo di attesa (minuti)")
plt.ylabel("Densità")
plt.legend()
plt.grid(True)
plt.show()

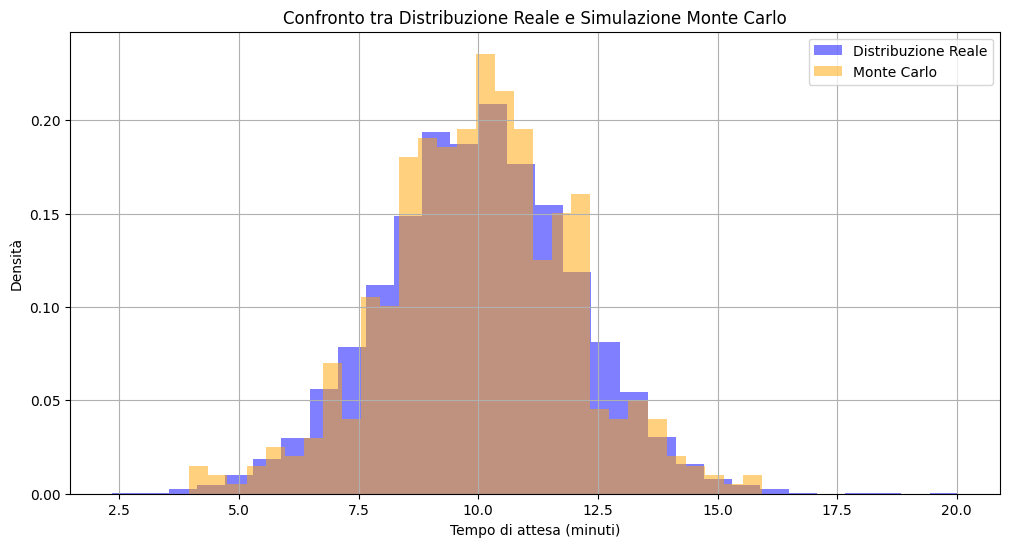
Distribuzioni condizionate

Le distribuzioni condizionate consentono di simulare dataset con correlazioni tra variabili. Questo è essenziale per generare dati sintetici che mantengono relazioni significative tra le dimensioni del dataset.

Esempio: Distribuzione normale multivariata

mean = [0, 0]  # Media per X e Y
covariance = [[1, 0.8], [0.8, 1]]  # Matrice di covarianza
data_multivariate = np.random.multivariate_normal(mean, covariance, 500)

# Visualizzazione
plt.scatter(data_multivariate[:, 0], data_multivariate[:, 1], alpha=0.6)
plt.title('Distribuzione Normale Multivariata')
plt.xlabel('X')
plt.ylabel('Y')
plt.axis('equal')
plt.show()

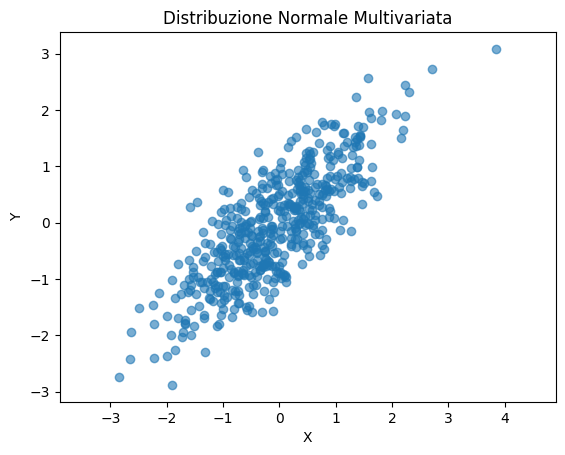
I metodi per la generazione di dati basati su distribuzioni statistiche offrono diversi vantaggi. Consentono un controllo completo, permettendo di definire parametri specifici che garantiscono la creazione di dati seguendo modelli statistici ben definiti. Inoltre, si distinguono per la loro flessibilità, adattandosi facilmente a diverse situazioni, come quelle che richiedono distribuzioni unimodali o multimodali. Dal punto di vista operativo, si rivelano particolarmente efficienti, poiché la generazione di dati è rapida e adeguata anche per dataset di grandi dimensioni.

Tuttavia, presentano anche alcuni limiti. Questi metodi funzionano al meglio con dataset caratterizzati da strutture statistiche semplici e chiare, ma risultano meno efficaci nel rappresentare relazioni complesse o non lineari. Inoltre, per ottenere risultati utili, è indispensabile una conoscenza approfondita delle distribuzioni e dei loro parametri, il che richiede una certa competenza tecnica da parte di chi li utilizza.

Esempio completo: Generazione di dati con relazioni specifiche

Creiamo un dataset sintetico con una relazione lineare rumorosa tra due variabili, ad esempio, altezza e peso.

# Parametri
np.random.seed(42)
n_samples = 1000
slope = 2.5  # Pendenza della relazione lineare
intercept = 50  # Intercetta
noise_level = 5  # Livello di rumore

# Generazione dati
heights = np.random.normal(170, 10, n_samples)  # Altezza con distribuzione normale
weights = slope * heights + intercept + np.random.normal(0, noise_level, n_samples)

# Visualizzazione
plt.scatter(heights, weights, alpha=0.6)
plt.title('Relazione Lineare Sintetica (Altezza vs Peso)')
plt.xlabel('Altezza (cm)')
plt.ylabel('Peso (kg)')
plt.show()

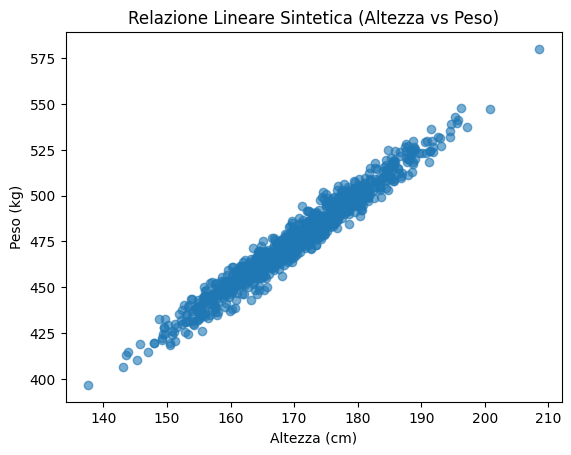
Generazione di dati con metodi di machine learning tradizionale

La generazione di dati sintetici tramite metodi di machine learning tradizionale è una tecnica molto utilizzata per ampliare dataset esistenti o per crearne di nuovi, mantenendo una struttura e una distribuzione plausibile. A differenza dei metodi avanzati, come le reti neurali profonde, questi approcci offrono semplicità di implementazione e un controllo diretto sulle caratteristiche dei dati generati.

Vuoi leggere di più su questo argomento?

Machine Learning Engineering

Andriy Burkov

Questo è IL libro di IA applicata più completo in circolazione. È pieno di best practice e modelli di progettazione per la creazione di soluzioni di apprendimento automatico affidabili e scalabili.

Compralo su Amazon

Gaussian Mixture Models (GMM)

I Gaussian Mixture Models (GMM) sono modelli probabilistici che rappresentano un dataset come una combinazione di diverse distribuzioni gaussiane. Ogni cluster del GMM corrisponde a una componente gaussiana. Questo approccio è particolarmente utile per generare dati che simulano dataset multi-classe.

Esempio: utilizzo dei GMM per generare un dataset sintetico basato su dati campione

import numpy as np
import matplotlib.pyplot as plt
from sklearn.mixture import GaussianMixture

# Dati originali: due cluster principali
np.random.seed(42)
data_original = np.concatenate([
    np.random.normal(loc=0, scale=1, size=(100, 2)),
    np.random.normal(loc=5, scale=1.5, size=(100, 2))
])

# Creazione del modello GMM
gmm = GaussianMixture(n_components=2, random_state=42)
gmm.fit(data_original)

# Generazione di nuovi dati sintetici
data_sintetici = gmm.sample(200)[0]

# Visualizzazione fianco a fianco
fig, axes = plt.subplots(1, 2, figsize=(12, 6), sharex=True, sharey=True)

# Grafico dei dati originali
axes[0].scatter(data_original[:, 0], data_original[:, 1], alpha=0.6, label="Dati Originali")
axes[0].legend()
axes[0].set_title("Dati Originali")
axes[0].grid(True)

# Grafico dei dati sintetici
axes[1].scatter(data_sintetici[:, 0], data_sintetici[:, 1], color='r', alpha=0.6, label="Dati Sintetici")
axes[1].legend()
axes[1].set_title("Dati Sintetici Generati con GMM")
axes[1].grid(True)

plt.tight_layout()
plt.show()

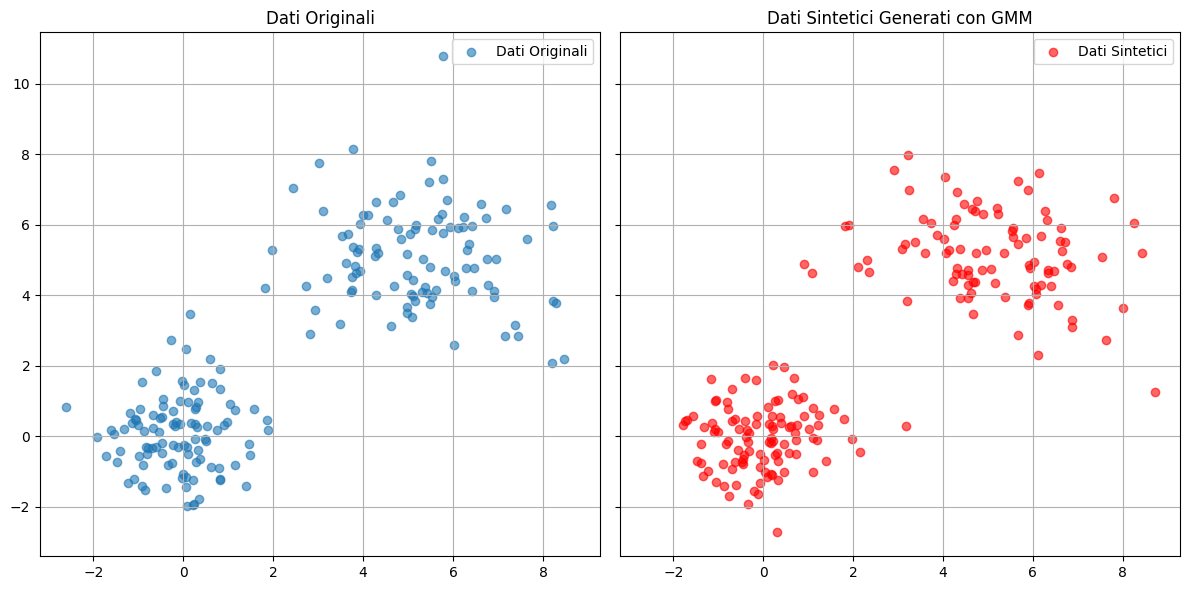
Tra i principali vantaggi di questo approccio vi è la possibilità di avere un controllo diretto sia sul numero di cluster che sulla varianza, permettendo un'analisi più mirata e personalizzata. Inoltre, si dimostra particolarmente efficace per dati che presentano una distribuzione multimodale, offrendo una buona approssimazione della loro struttura.

Tuttavia, ci sono anche alcune limitazioni da considerare. Questo metodo è adatto esclusivamente a dataset che possono essere modellati con distribuzioni gaussiane, il che ne restringe il campo di applicazione. Inoltre, richiede di determinare in anticipo il numero ottimale di componenti, cioè il numero di cluster, un aspetto che può rappresentare una sfida nei contesti più complessi.

Alberi di decisione generativi

Gli alberi di decisione generativi costruiscono relazioni condizionali tra variabili. Possono essere utilizzati per generare dati che rispettano schemi complessi, come vincoli logici o dipendenze tra variabili.

Esempio: Generazione di un dataset sintetico basato su regole condizionali.

from sklearn.tree import DecisionTreeClassifier
import pandas as pd

# Creazione di un dataset semplice
np.random.seed(42)
data_original = pd.DataFrame({
    'Feature1': np.random.choice([0, 1], size=100),
    'Feature2': np.random.choice([0, 1], size=100),
    'Label': np.random.choice([0, 1], size=100)
})

# Costruzione dell'albero di decisione
X = data_original[['Feature1', 'Feature2']]
y = data_original['Label']
tree = DecisionTreeClassifier(max_depth=3, random_state=42)
tree.fit(X, y)

# Generazione di nuovi dati
data_sintetici = pd.DataFrame({
    'Feature1': np.random.choice([0, 1], size=100),
    'Feature2': np.random.choice([0, 1], size=100)
})
data_sintetici['Label'] = tree.predict(data_sintetici)

print("Dati sintetici generati:\n", data_sintetici.head())

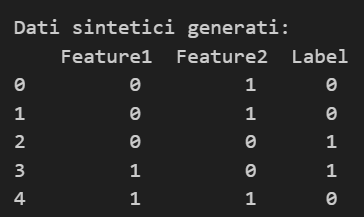
Tra i principali vantaggi di questo approccio c'è la sua flessibilità, che permette di modellare anche regole complesse. Si rivela particolarmente utile quando si vuole replicare dataset che presentano relazioni condizionali tra le variabili, garantendo una coerenza nelle strutture dei dati.

Tuttavia, ci sono anche dei limiti da considerare. Questo metodo può rischiare di sovradattarsi ai dati originali (overfitting), riducendo così la capacità di generalizzazione. Inoltre, non è la soluzione più indicata per generare dataset caratterizzati da un'elevata variabilità, dove risulta più difficile mantenere la rappresentatività dei dati.

Generazione di dati sintetici con LLM (Large Language Models)

I Large Language Models (LLM) rappresentano una delle tecnologie più avanzate per la generazione di dati sintetici. Essi combinano capacità di comprensione e generazione del linguaggio naturale con la potenza del deep learning, rendendoli strumenti ideali per creare dataset strutturati, coerenti e personalizzati. In questa sezione, esploreremo come utilizzare LLM per generare dati sintetici, con esempi pratici e codice Python per dimostrare la loro applicazione.

LLM come GPT o BERT possono essere addestrati o adattati a creare dati sintetici grazie alla loro capacità di:

1. Comprendere il contesto: Possono analizzare e generare dati con relazioni complesse, adattandosi a specifici contesti.
2. Personalizzazione: Offrono la possibilità di generare dati che rispettano regole o schemi definiti dall'utente.
3. Efficacia su dati non strutturati: Sono particolarmente potenti per generare dati testuali e tabellari.

Esempio: Creazione di un Dataset Tabellare

Consideriamo un caso in cui vogliamo generare un dataset tabellare per un'applicazione di marketing, contenente informazioni sui clienti come età, città e reddito annuale.

Step 1: Definire il Prompt

Un prompt efficace guida l'LLM nel creare dati coerenti. Ecco un esempio di prompt:

"Generate a dataset with 10 rows and 4 columns:\n"
"Job (a string representing a person's job), "
"Age (an integer between 18 and 75), "
"Country (a string representing a country name), "
"and Score (a floating-point number between 0 and 100).\n\n"
"Job | Age | Country | Score\n"


"---------------------------------\n"
"Teacher | 30 | USA | 88.5\n"
"Engineer | 45 | UK | 92.3\n"
"Nurse | 28 | Canada | 75.4\n"
"Artist | 33 | France | 68.9\n"
"Doctor | 50 | Germany | 85.1\n"

Step 2: Utilizzare Python per generare i dati

Con librerie come transformers, possiamo interagire con modelli pre-addestrati per generare il dataset:

from transformers import GPTNeoForCausalLM, GPT2Tokenizer
import torch
import re

# Caricare il tokenizzatore ed il modello da hugging face
model_name = "EleutherAI/gpt-neo-1.3B"
tokenizer = GPT2Tokenizer.from_pretrained(model_name)
tokenizer.pad_token = tokenizer.eos_token
model = GPTNeoForCausalLM.from_pretrained(model_name)
model.config.pad_token_id = tokenizer.eos_token_id
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model.to(device)
model.eval()

prompt = (
    "Generate a dataset with 10 rows and 4 columns:\n"
    "Job (a string representing a person's job), "
    "Age (an integer between 18 and 75), "
    "Country (a string representing a country name), "
    "and Score (a floating-point number between 0 and 100).\n\n"
    "Job | Age | Country | Score\n"
    "---------------------------------\n"
    "Teacher | 30 | USA | 88.5\n"
    "Engineer | 45 | UK | 92.3\n"
    "Nurse | 28 | Canada | 75.4\n"
    "Artist | 33 | France | 68.9\n"
    "Doctor | 50 | Germany | 85.1\n"
)

# Encoding del prompt
inputs = tokenizer(prompt, return_tensors="pt", padding=True).to(device)
input_ids = inputs['input_ids']
attention_mask = inputs['attention_mask']

# Generazione del testo
output = model.generate(
    input_ids=input_ids,
    attention_mask=attention_mask,
    max_length=input_ids.shape[1] + 200,
    num_return_sequences=1,
    no_repeat_ngram_size=2,
    do_sample=False,
    temperature=0.7,
    pad_token_id=tokenizer.eos_token_id
)

# Decodifica dell'output
generated_text = tokenizer.decode(output[0], skip_special_tokens=True)
print(generated_text)

# Estrazione del pattern di lettura
data_pattern = re.compile(
    r"([A-Za-z\s]+)\s*\|\s*(\d{1,2})\s*\|\s*([A-Za-z\s]+)\s*\|\s*(\d{1,3}\.\d+)"
)
matches = data_pattern.findall(generated_text)

print("\nExtracted Data:")
for match in matches:
    print(f"Job: {match[0].strip()}, Age: {match[1]}, Country: {match[2].strip()}, Score: {match[3]}")

Extracted Data:
Job: Teacher, Age: 30, Country: USA, Score: 88.5
Job: Engineer, Age: 45, Country: UK, Score: 92.3
Job: Nurse, Age: 28, Country: Canada, Score: 75.4
Job: Artist, Age: 33, Country: France, Score: 68.9
Job: Doctor, Age: 50, Country: Germany, Score: 85.1
Job: Manager, Age: 25, Country: Spain, Score: 77.8
Job: Salesperson, Age: 35, Country: Japan, Score: 73.6
Job: Driver, Age: 20, Country: Australia, Score: 71.2
Job: Clerk, Age: 40, Country: India, Score: 70.7
Job: Student, Age: 24, Country: China, Score: 69.0
Job: Baker, Age: 22, Country: Brazil, Score: 66.75
Job: Maid, Age: 23, Country: Italy, Score: 65.25
Job: Cook, Age: 21, Country: Greece, Score: 64.15
Job: Housewife, Age: 26, Country: Turkey, Score: 63.85
Job: Fisherman, Age: 29, Country: Russia, Score: 62.65
Job: Porter, Age: 27, Country: South Africa, Score: 61.45
Job: Sailor, Age: 32, Country: United States, Score: 60.35
Job: Soldier, Age: 31, Country: Sweden, Score: 59.05
Job: Police, Age: 34, Country: Netherlands, Score: 58.95
Job: Paramedic, Age: 36, Country: Belgium, Score: 57.55
Job: Construction worker, Age: 37, Country: Denmark, Score: 56.40
Job: Electrician, Age: 38, Country: Norway, Score: 55.10

Gli LLM (Large Language Models) offrono numerosi vantaggi che li rendono strumenti estremamente versatili. Innanzitutto, sono caratterizzati da una grande flessibilità: sono in grado di generare sia dati strutturati che non strutturati, adattandosi a molteplici esigenze. Inoltre, la loro integrazione nei flussi di lavoro è resa semplice grazie all’uso di API e librerie Python, che consentono un’implementazione rapida ed efficace.

Un altro aspetto positivo è la possibilità di personalizzazione: i prompt possono essere facilmente modificati per soddisfare specifiche necessità, rendendo questi modelli ancora più utili in contesti mirati.

Tuttavia, è importante considerare alcuni limiti e aspetti critici. La qualità dei dati generati, ad esempio, dipende fortemente dalla formulazione del prompt e dalle impostazioni del modello utilizzato.

Un altro elemento da tenere a mente è la presenza di bias: poiché i modelli apprendono dai dati su cui sono stati addestrati, è possibile che riproducano pregiudizi o distorsioni già presenti in quei dati. Infine, il costo rappresenta un fattore rilevante, soprattutto in ambiti produttivi dove l’uso intensivo degli LLM può comportare spese significative.

Generazione di dati con strutture e relazioni specifiche

La generazione di dati sintetici con strutture e relazioni specifiche è una pratica avanzata che richiede tecniche per creare dataset artificiali rispettando vincoli complessi. Questa metodologia è essenziale per simulazioni in cui i dati sintetici devono rappresentare scenari reali o completare dataset esistenti senza comprometterne l'integrità. 

Generare dati con strutture ben definite è un'attività molto utile in numerosi contesti. Ad esempio, nelle simulazioni finanziarie è importante produrre serie temporali che rispettino determinate correlazioni tra variabili. In ambito fisico, è necessario creare dati che seguano specifiche equazioni o leggi naturali. In bioinformatica, invece, è fondamentale costruire dataset che tengano conto di vincoli biologici o chimici propri del contesto di studio.

L'obiettivo principale è quello di creare dati sintetici che non siano solo statisticamente rappresentativi, ma che rispettino anche le regole e le relazioni caratteristiche del dominio applicativo a cui si riferiscono.

Gestione di relazioni complesse

Esempio: Generazione di dati con somme fisse

Un caso comune è generare variabili che rispettino un vincolo di somma totale, ad esempio, il budget tra diversi dipartimenti.

import numpy as np
import pandas as pd
 
# Numero di osservazioni e categorie
n_observations = 100
n_categories = 3
 
# Somma totale per ogni osservazione
total_sum = 100
 
# Generazione di dati casuali
data = np.random.dirichlet(np.ones(n_categories), size=n_observations) * total_sum
 
# Creazione di un DataFrame
df = pd.DataFrame(data, columns=[f"Categoria_{i+1}" for i in range(n_categories)])
df["Totale"] = df.sum(axis=1)
 
print("Esempio di dataset generato con somma fissa:")
print(df.head())

>>>

Esempio di dataset generato con somma fissa:
   Categoria_1  Categoria_2  Categoria_3  Totale
0    58.673361    34.972747     6.353891   100.0
1    16.882673    14.145658    68.971669   100.0
2    71.446625    10.170256    18.383118   100.0
3    57.066341    37.334702     5.598957   100.0
4    15.686990     3.622839    80.690171   100.0

La funzione dirichlet è utilizzata per generare proporzioni casuali, ciascuna delle quali rappresenta una frazione di un totale. Queste proporzioni, una volta calcolate, vengono scalate in modo che la loro somma sia pari a un valore specifico definito come total_sum. In questo modo, i dati prodotti dalla funzione mantengono il vincolo fondamentale che prevede che la somma complessiva delle proporzioni sia esattamente uguale al valore target indicato.

Esempio: dati con correlazioni predefinite

Un'altra esigenza comune è generare dati sintetici con correlazioni specifiche tra variabili.

from scipy.stats import norm

# Dimensione del dataset
n_samples = 1000

# Matrice di correlazione desiderata
correlation_matrix = np.array([[1.0, 0.8, 0.5], [0.8, 1.0, 0.3],[0.5, 0.3, 1.0]])

# Creazione di dati correlati
mean = [0, 0, 0]
data = np.random.multivariate_normal(mean, correlation_matrix, size=n_samples)

# Conversione in DataFrame
df_corr = pd.DataFrame(data, columns=["Variabile_1", "Variabile_2", "Variabile_3"])
print(df_corr.corr())

>>>

             Variabile_1  Variabile_2  Variabile_3
Variabile_1     1.000000     0.784861     0.490152
Variabile_2     0.784861     1.000000     0.263210
Variabile_3     0.490152     0.263210     1.000000

La funzione multivariate_normal permette di generare dati che seguono una distribuzione multivariata, rispettando le correlazioni stabilite dalla matrice di correlazione fornita come input.

Modelli basati su grafi

I modelli basati su grafi sono utili per simulare reti sociali, transazioni, o flussi di informazioni.

import networkx as nx
import pandas as pd
import matplotlib.pyplot as plt

# Creazione di un grafo casuale
n_nodes = 10
p_connection = 0.3
graph = nx.erdos_renyi_graph(n_nodes, p_connection)

# Conversione in DataFrame
edges = nx.to_pandas_edgelist(graph)
print("Lista di connessioni (archi):")
print(edges)

# Visualizzazione del grafo
plt.figure(figsize=(8, 6))
nx.draw(graph, with_labels=True, node_color='lightblue', edge_color='gray', node_size=700, font_size=10)
plt.title("Rappresentazione del Grafo Casuale")
plt.show()

>>>

Lista di connessioni (archi):
   source  target
0       0       3
1       0       8
2       0       9
3       1       3
4       1       9
5       2       9
6       3       7
7       4       7
8       5       8
9       6       7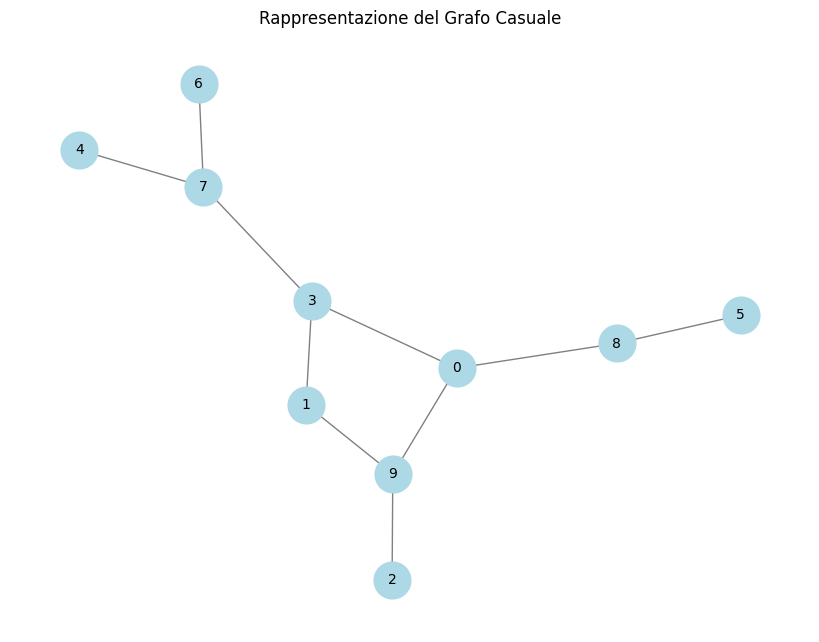

Le applicazioni principali di questo contesto includono, da un lato, la simulazione delle reti sociali, che permette di analizzare e prevedere dinamiche di interazione e comportamenti collettivi all'interno di comunità virtuali o reali. Dall'altro lato, troviamo la modellazione dei flussi di dati in sistemi distribuiti, un'attività cruciale per comprendere, ottimizzare e gestire la trasmissione delle informazioni in ambienti tecnologici complessi e interconnessi.

Modelli autoregressivi per serie temporali

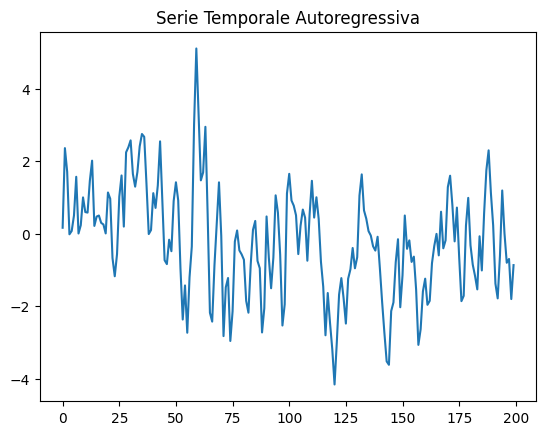
Le serie temporali autoregressive sono usate per simulare dati con dipendenze temporali.

from statsmodels.tsa.arima_process import ArmaProcess
 
# Definizione dei parametri AR e MA
ar_params = np.array([1, -0.5])
ma_params = np.array([1, 0.4])
model = ArmaProcess(ar=ar_params, ma=ma_params)
 
# Generazione della serie temporale
n_points = 200
time_series = model.generate_sample(nsample=n_points)
 
# Visualizzazione
import matplotlib.pyplot as plt
plt.plot(time_series)
plt.title("Serie Temporale Autoregressiva")
plt.show()

Considerazioni etiche e limiti nella generazione di dati sintetici

La generazione di dati sintetici offre una soluzione innovativa e flessibile per superare le sfide legate alla disponibilità, qualità e protezione dei dati reali, ma pone rilevanti questioni etiche e operative che richiedono una valutazione attenta.

Un primo problema riguarda il rischio di similitudine eccessiva con i dati reali. Se i dati sintetici sono troppo fedeli alle fonti originali, possono rivelare informazioni sensibili sugli individui. Inoltre, la combinazione di questi dati con altri dataset può permettere di individuare correlazioni che facilitano la re-identificazione.

Un'altra criticità è il potenziale trasferimento o amplificazione di bias presenti nei dati originali. I dati sintetici potrebbero infatti mantenere squilibri di classe o attributi se non vengono applicati controlli rigorosi durante la loro generazione. Inoltre, durante il processo di creazione, è possibile introdurre nuovi bias non intenzionali, aggravando il problema.

La validità e l'usabilità dei dati sintetici rappresentano un'ulteriore sfida. Per essere utili, i dati devono rispettare le relazioni e i vincoli propri dei dati reali, come somme o sequenze temporali. Se queste caratteristiche mancano, i dati sintetici possono risultare inapplicabili. Inoltre, modelli di machine learning addestrati su dati sintetici rischiano di non generalizzarsi adeguatamente ai contesti reali.

Dal punto di vista normativo ed etico, è essenziale che la generazione di dati sintetici rispetti le leggi sulla protezione dei dati, come il GDPR in Europa o il CCPA negli Stati Uniti. Questo implica una gestione rigorosa dei dati originali e la conformità ai requisiti legali in ogni fase del processo.

Conclusioni

La generazione di dati sintetici si sta affermando come un elemento cruciale nella data science e nel machine learning, soprattutto in situazioni dove la disponibilità di dati reali è limitata da vincoli di privacy, bias o mancanza di rappresentatività. Tuttavia, la sua efficacia dipende dalla scelta delle tecniche più appropriate e dalla consapevolezza dei limiti e delle implicazioni etiche che comporta.

Tra le tecniche disponibili, quelle probabilistiche si rivelano semplici ed efficaci per rappresentare distribuzioni lineari, pur mostrando limiti con dati complessi. I metodi tradizionali di Machine Learning, offrono un buon compromesso tra semplicità e capacità di catturare strutture più articolate. I modelli di linguaggio avanzati, come i Large Language Models, si distinguono per la loro flessibilità, consentendo la generazione di dati altamente realistici e complessi, ideali per contesti come simulazioni, analisi tabellari e testi.

Per massimizzare il valore dei dati sintetici, è fondamentale personalizzare le strategie di generazione in base alle esigenze specifiche, monitorare costantemente la qualità dei dati prodotti e confrontarli con quelli reali. Occorre anche integrare controlli per mitigare bias e violazioni della privacy, nonché aggiornarsi sulle rapide evoluzioni tecnologiche nel campo.