Confronto tra modelli per l'analisi delle serie temporali storiche economiche

Nel panorama della data science, la previsione dei mercati finanziari rappresenta una delle sfide più complesse e stimolanti. Tra indici economici globali, il Dow Jones Industrial Average (DJIA) spicca come un indicatore chiave della salute economica e delle fluttuazioni di mercato.

Con il rapido sviluppo di strumenti e metodologie per l’analisi di serie temporali, tre approcci principali sono emersi come protagonisti nella previsione dei mercati: i modelli statistici tradizionali come AR, ARIMA, algoritmi specifici per business come Facebook Prophet, e tecniche avanzate di deep learning come le reti neurali Long Short-Term Memory (LSTM). Ogni metodo porta con sé punti di forza distintivi e sfide che ne influenzano l’applicabilità e la precisione.

Questo articolo si propone di confrontare le performance di AR, ARIMA, Prophet e LSTM nella previsione delle principali stock del DJIA, esaminando i loro vantaggi, limiti e i contesti di utilizzo ottimali. Attraverso un’analisi strutturata, esploreremo la preparazione dei dati, l’implementazione dei modelli e la valutazione delle loro prestazioni, offrendo un quadro completo per scegliere la tecnica migliore in base alle esigenze specifiche.

L’obiettivo non è solo quello di determinare quale modello predice meglio il valore di chiusura delle stock, ma anche di fornire raccomandazioni pratiche per l’adozione strategica di queste tecniche.

Il dataset

Il Dow Jones Industrial Average è un indice di borsa ponderato sulla base del prezzo, composto da 30 delle maggiori società pubbliche degli Stati Uniti. Nel panorama della finanza globale, il Dow Jones Industrial Average (DJIA) rappresenta uno degli indici più longevi e influenti. Creato nel 1896, è spesso utilizzato come barometro della salute economica degli Stati Uniti e, più in generale, dell'economia globale.  Creato da Charles Dow, cofondatore del Wall Street Journal e di Dow Jones & Company. L'indice inizialmente comprendeva 12 aziende, principalmente del settore industriale, che dominava l'economia statunitense dell'epoca. Nel corso del tempo, il DJIA ha subito numerose trasformazioni per riflettere i cambiamenti economici e industriali. Noi per semplicità useremo soltanto le 4 stock più note: Amazon, Apple, McDonald's e Microsoft.

Dove reperire i dati storici del DJIA

Fonti gratuite

1. Yahoo Finance
   Yahoo Finance offre dati storici dettagliati, inclusi prezzi di apertura, chiusura, massimi, minimi e volumi di scambio. È possibile scaricare i dati in formato CSV per analisi offline.
   • URL: finance.yahoo.com
   • Funzionalità: Personalizzazione degli intervalli temporali e download diretto.
2. Google Finance
   Una piattaforma user-friendly che consente di visualizzare grafici interattivi e analizzare i movimenti storici dell'indice. Tuttavia, il download diretto dei dati può essere più limitato rispetto a Yahoo Finance.

Librerie Python

Per chi utilizza strumenti di analisi dei dati, esistono librerie Python dedicate al recupero e alla manipolazione dei dati finanziari:

• yfinance: Una libreria open source che consente di accedere ai dati di Yahoo Finance.

import yfinance as yf
import pandas as pd

# List of stock symbols to analyze
stocks = ['AAPL', 'AMZN', 'MCD', 'MSFT']

# Download historical stock data for the specified period
data = yf.download(stocks, start='2022-01-01', end='2024-12-31')

# Convert the multi-index (Date, Ticker) into columns for easier manipulation
data = data.stack(level='Ticker').reset_index()

# Rename the columns to follow a consistent and descriptive format
data.rename(
    columns={
        'Date': 'Date',          # Date of the stock data
        'Ticker': 'Stock',       # Stock symbol (e.g., AAPL, AMZN)
        'Open': 'Open',          # Opening price of the stock
        'High': 'High',          # Highest price of the stock
        'Low': 'Low',            # Lowest price of the stock
        'Close': 'Close',        # Closing price of the stock
        'Adj Close': 'Adj Close', # Adjusted closing price of the stock
        'Volume': 'Volume',      # Trading volume of the stock
    },
    inplace=True,
)

# Reorder the columns in a logical sequence
data = data[['Date', 'Open', 'High', 'Low', 'Close', 'Adj Close', 'Volume', 'Stock']]

# Sort the data first by Stock and then by Date for better organization
data = data.sort_values(by=['Stock', 'Date']).reset_index(drop=True)

# Extract the unique list of stock symbols from the dataset
stock_list = data['Stock'].unique()

# Define the columns to be used as features for further analysis or modeling
feature_columns = ['Open', 'High', 'Low', 'Volume']

# Display the first few rows of the transformed DataFrame for verification
print(data.head())


>>>

Price       Date      Open      High       Low     Close  Adj Close  \
0     2004-08-19  0.562679  0.568929  0.542143  0.548393   0.462595   
1     2004-08-20  0.548393  0.553393  0.544464  0.550000   0.463951   
2     2004-08-23  0.551071  0.558393  0.546429  0.555000   0.468169   
3     2004-08-24  0.558214  0.570536  0.556964  0.570536   0.481274   
4     2004-08-25  0.569107  0.591964  0.566607  0.590179   0.497844   

Price     Volume Stock  
0      388920000  AAPL  
1      316780800  AAPL  
2      254660000  AAPL  
3      374136000  AAPL  
4      505618400  AAPL  

Cross-Walk Validation nelle serie storiche

La cross-walk validation è una tecnica di validazione utilizzata principalmente per valutare le prestazioni di un modello predittivo nel contesto delle serie storiche. Si tratta di una variazione della più comune validazione incrociata (cross-validation), ma è adattata per tener conto della natura sequenziale dei dati temporali, evitando violazioni del principio causale (cioè il modello non deve mai “vedere” dati futuri durante l’addestramento).

In una serie temporale, i dati sono organizzati in ordine cronologico, rendendo necessario separare chiaramente i dati utilizzati per l’addestramento da quelli utilizzati per il testing. La cross-walk validation segue questi passaggi principali:

1. Divisione della Serie Temporale in Finestra Temporali (Walks):
   • La serie storica viene suddivisa in finestra temporali sovrapposte o sequenziali. Ogni finestra comprende un intervallo di dati per l’addestramento e un intervallo successivo per la validazione.
   • Ad esempio, si potrebbe utilizzare un periodo di tre anni per l’addestramento e il quarto anno per il test, spostando la finestra avanti di un anno a ogni iterazione.
2. Iterazioni Multiple:
   • Si iterano più “walks”, facendo avanzare la finestra temporale lungo i dati. Questo assicura che il modello venga valutato su più segmenti della serie, migliorando la robustezza della valutazione.
3. Predizioni e Calcolo delle Metriche:
   • Per ciascuna finestra, il modello è addestrato sui dati di addestramento e valutato su quelli di validazione. Le metriche di performance (ad esempio RMSE) vengono calcolate per ogni walk e poi aggregate per ottenere una stima complessiva delle prestazioni.

Perché la Cross-Walk Validation è importante nelle serie storiche

1. Rispettare la Sequenzialità dei Dati:
   • Nelle serie temporali, i dati futuri dipendono dai dati passati. La cross-walk validation assicura che il modello non utilizzi informazioni dal futuro durante l’addestramento, rispettando la realtà dei dati temporali.
2. Valutazione Robusta e Generalizzabile:
   • Utilizzando diverse suddivisioni temporali, questa tecnica riduce il rischio di overfitting a un particolare segmento temporale. I risultati ottenuti sono più affidabili e indicativi delle prestazioni su dati non visti.
3. Adattabilità ai Cambiamenti Temporali:
   • Le serie storiche possono essere soggette a cambiamenti strutturali (es. stagionalità, trend o eventi esterni). La cross-walk validation permette di testare il modello su diversi periodi, valutandone la capacità di adattarsi a tali variazioni.
4. Riduzione della Varianza nelle Stime:
   • Aggregando le performance su più iterazioni, si ottiene una stima più accurata e stabile delle capacità del modello, mitigando l’impatto di fluttuazioni specifiche in uno o pochi periodi temporali.

La cross-walk validation rappresenta un approccio essenziale per la validazione dei modelli su serie temporali, garantendo una valutazione realistica e robusta delle prestazioni predittive. Questo metodo consente di progettare modelli più affidabili, migliorandone la capacità di generalizzare su dati futuri e rafforzandone l’applicabilità nel mondo reale.

Modellazione dei dati

Il Modello Autoregressivo (AR)

Nel mondo dell'analisi delle serie temporali, il modello autoregressivo (AR) rappresenta uno strumento statistico fondamentale e ampiamente utilizzato. Grazie alla sua semplicità e interpretabilità, il modello AR è particolarmente efficace nel catturare la dipendenza lineare tra i valori di una variabile e i suoi valori osservati in momenti precedenti.

Il modello AR assume che il valore corrente di una variabile al tempo \( t \), indicato con \( Y(t) \), sia determinato da una combinazione lineare dei suoi valori passati, fino a un certo numero di ritardi \( p \) (ordine del modello), e da un termine di errore casuale \( \epsilon(t) \).

Vantaggi del Modello AR

1. Semplicità e Interpretabilità: Il modello AR è relativamente semplice da comprendere e implementare. I coefficienti ϕ forniscono un'indicazione diretta dell'influenza dei valori passati sulla variabile attuale.
2. Efficacia su dati stazionari: Se la serie temporale è stazionaria (ossia non presenta trend sistematici nel tempo), il modello AR può fornire previsioni accurate.
3. Adatto a previsioni a breve termine: Il modello è particolarmente efficace per orizzonti temporali brevi.

Limiti del Modello AR

Nonostante i suoi punti di forza, il modello AR presenta alcune limitazioni:

• Assunzione di linearità: Il modello presume una relazione lineare tra i valori della variabile. Tuttavia, molte serie temporali reali possono presentare comportamenti non lineari.
• Sensibilità alla stazionarietà: Il modello richiede che la serie sia stazionaria. Se non lo è, è necessario trasformare i dati (ad esempio, attraverso la differenziazione).
• Residui non casuali: Se l’errore ε(t) presenta una struttura non casuale, il modello AR può risultare inadeguato.

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from statsmodels.tsa.ar_model import AutoReg

# Simple preprocessor function
def preprocess_stock_data(stock_data):
    return stock_data['Close'].values, stock_data['Date'].values

# Simplified AutoReg Model
class AutoRegForecast:
    def __init__(self, lags, rolling_window, num_future_forecasts):
        self.lags = lags
        self.rolling_window = rolling_window
        self.num_future_forecasts = num_future_forecasts

    def fit(self, target_y):
        self.target_y = target_y

    def predict(self, dates):
        if not self.num_future_forecasts:
            raise ValueError("Specify num_future_forecasts before calling predict.")

        # Rolling historical predictions
        rolling_preds = [
            AutoReg(self.target_y[i - self.rolling_window:i], lags=self.lags).fit().forecast(steps=1)[0]
            for i in range(self.rolling_window, len(self.target_y))
        ]
        hist_dates = dates[self.rolling_window:]

        # Future predictions
        future_model = AutoReg(self.target_y[-self.rolling_window:], lags=self.lags).fit()
        future_preds = future_model.forecast(steps=self.num_future_forecasts)
        future_dates = pd.date_range(start=pd.to_datetime(dates[-1]) + pd.Timedelta(days=1),
                                     periods=self.num_future_forecasts)

        return np.array(rolling_preds), hist_dates, future_preds, future_dates

# Process and forecast multiple stocks
def process_stocks(data, stock_list, rolling_window, lags, num_future_forecasts):
    predictions = {}
    results = []

    for stock in stock_list:
        print(f"Processing stock: {stock}")
        stock_data = data[data['Stock'] == stock]
        target_y, dates = preprocess_stock_data(stock_data)

        model = AutoRegForecast(lags, rolling_window, num_future_forecasts)
        model.fit(target_y)
        hist_preds, hist_dates, fut_preds, fut_dates = model.predict(dates)

        # Calculate RMSE for historical predictions
        true_values = target_y[rolling_window:]
        rmse = np.sqrt(np.mean((hist_preds - true_values) ** 2))
        results.append([stock, rmse])
        print(f"RMSE for {stock}: {rmse}")

        predictions[stock] = (hist_dates, hist_preds, fut_dates, fut_preds)

    return results, predictions

# Plot predictions
def plot_predictions(data, predictions, stock_list):
    fig, axes = plt.subplots(nrows=(len(stock_list) + 1) // 2, ncols=2, figsize=(16, len(stock_list) * 2))
    axes = axes.flatten() if len(stock_list) > 1 else [axes]

    for idx, stock in enumerate(stock_list):
        ax = axes[idx]
        stock_df = data[data['Stock'] == stock]
        stock_df = stock_df[pd.to_datetime(stock_df['Date']) >= pd.Timestamp('2024-06-01')]

        hist_dates, hist_preds, fut_dates, fut_preds = predictions[stock]

        hist_mask = pd.to_datetime(hist_dates) >= pd.Timestamp('2024-06-01')
        hist_dates, hist_preds = hist_dates[hist_mask], hist_preds[hist_mask]

        ax.plot(stock_df['Date'], stock_df['Close'], label='Historical Prices', color='blue')
        ax.plot(hist_dates, hist_preds, label='Historical Forecasts', color='green', alpha=0.75)
        ax.plot(fut_dates, fut_preds, label='Future Forecasts', color='red', linestyle='--')

        ax.set_title(stock)
        ax.set_xlabel('Date')
        ax.set_ylabel('Price')
        ax.legend()
        ax.grid(True)

    plt.tight_layout()
    plt.show()

# Example usage
results, predictions = process_stocks(data, stock_list, rolling_window=120, lags=15, num_future_forecasts=10)
plot_predictions(data, predictions, stock_list)

>>>

Processing stock: AAPL
RMSE for AAPL: 2.9898124340328995
Processing stock: AMZN
RMSE for AMZN: 3.289917243950366
Processing stock: MCD
RMSE for MCD: 3.145640518282811
Processing stock: MSFT
RMSE for MSFT: 5.524588191096785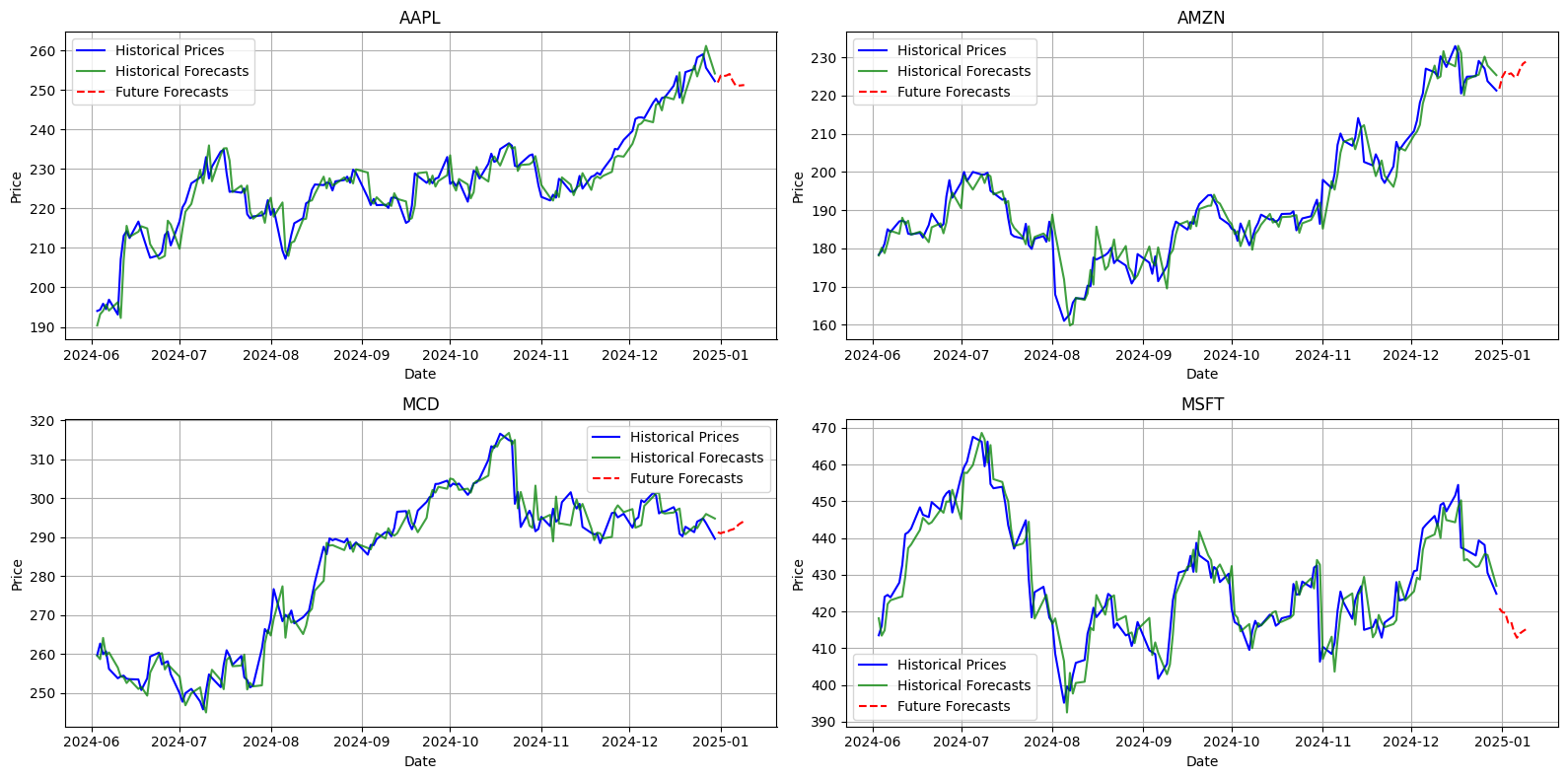

I risultati delle previsioni sui titoli, ottenuti tramite il modello autoregressivo (AR), mostrano performance variabili tra le diverse azioni, misurate attraverso l’errore quadratico medio (RMSE), dove valori più bassi indicano una maggiore accuratezza.

Le azioni con i migliori risultati includono AAPL (RMSE: 2.99) e MCD (RMSE: 3.15), suggerendo che i loro andamenti storici siano più facilmente prevedibili. Questa maggiore prevedibilità potrebbe dipendere da una volatilità relativamente contenuta o da trend più regolari. Anche AMZN (RMSE: 3.29) ha mostrato un livello di accuratezza accettabile, confermando la capacità del modello di adattarsi a titoli con caratteristiche simili.

Al contrario, per azioni come MSFT (RMSE: 5.52), il modello ha avuto maggiori difficoltà nel catturare le dinamiche di mercato, probabilmente a causa di una volatilità più elevata o di comportamenti storicamente meno regolari. Questi risultati evidenziano come le caratteristiche intrinseche delle diverse azioni possano influenzare le prestazioni del modello predittivo.

Nel complesso, il modello autoregressivo si è dimostrato efficace per alcune azioni con andamenti più lineari, ma ha evidenziato limitazioni nel gestire titoli caratterizzati da maggiore complessità e volatilità nei movimenti di mercato. Questi risultati suggeriscono che una futura ottimizzazione del modello potrebbe migliorare la capacità di previsione per i titoli più imprevedibili.

Il modello autoregressivo (AR) rimane uno strumento robusto ed efficace per la previsione delle serie temporali, specialmente quando le relazioni tra i dati sono lineari e i residui sono indipendenti e casuali. La sua semplicità, interpretabilità e adattabilità lo rendono ideale per molte applicazioni pratiche, come l'analisi finanziaria, economica e industriale. Tuttavia, è fondamentale valutare attentamente la stazionarietà dei dati e considerare i limiti del modello, adottando eventualmente tecniche alternative per catturare relazioni più complesse.

ARIMA: Un modello statistico tradizionale

Nel panorama della previsione delle serie temporali, i modelli di machine learning e statistici offrono diverse prospettive per interpretare dati complessi. Tra questi, il modello ARIMA (AutoRegressive Integrated Moving Average) rappresenta un approccio tradizionale ma ampiamente utilizzato grazie alla sua semplicità e interpretabilità.

L’ARIMA è un modello progettato per serie temporali stazionarie, ovvero dati il cui comportamento statistico non varia nel tempo. Si basa su tre componenti principali:

• AR (AutoRegressive): cattura la dipendenza lineare tra il valore attuale e i valori passati.
• I (Integrated): rappresenta la differenziazione necessaria per rendere i dati stazionari.
• MA (Moving Average): considera le dipendenze tra il valore osservato e gli errori di previsione passati.

Questa combinazione di autoregressione, differenziazione e media mobile rende ARIMA un modello potente per analizzare e prevedere serie temporali con caratteristiche ben definite. La combinazione delle componenti AR, I e MA consente al modello di adattarsi a diverse strutture delle serie temporali.

Vantaggi di ARIMA

1. Efficace su dati stazionari: L’ARIMA è particolarmente adatto per dati in cui i trend o le stagionalità possono essere rimossi attraverso trasformazioni come la differenziazione. Ad esempio, una serie temporale del DJIA può mostrare una crescita lineare o una stagionalità annuale che il modello può gestire efficacemente.
2. Interpretabilità: La semplicità del modello consente di analizzare facilmente l’influenza di ciascuna componente (AR, I, MA) sul comportamento della serie. Questo è un vantaggio significativo rispetto a modelli complessi come le reti neurali, dove l’interpretazione diventa più difficile.
3. Adattabilità a brevi orizzonti temporali: Per previsioni a breve termine, l’ARIMA offre un’accuratezza spesso comparabile a modelli più avanzati, evitando complessità computazionali.

Limiti di ARIMA

1. Sensibilità ai dati non stazionari: Sebbene il modello includa un componente per la differenziazione, non sempre riesce a catturare correttamente le caratteristiche di serie con trend complessi o cambiamenti strutturali nel tempo. Questo è particolarmente critico per serie temporali finanziarie, dove i trend possono essere influenzati da eventi macroeconomici imprevisti.
2. Limitazioni su serie non lineari: ARIMA presuppone che la relazione tra variabili sia lineare. Tuttavia, molte serie temporali, incluso il DJIA, possono presentare comportamenti non lineari difficili da modellare con ARIMA.
3. Richiede pre-processing significativo: La necessità di stazionare i dati implica operazioni preliminari come test di stazionarietà (ad esempio, il test di Dickey-Fuller) e identificazione manuale dei parametri (p, d, q). Queste attività possono essere laboriose e soggette a errori.

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from statsmodels.tsa.arima.model import ARIMA

# Simple preprocessing function
def preprocess_stock_data(stock_data, feature_columns=None):
    return stock_data['Close'].values, stock_data['Date'].values

# Simplified ARIMA Model
class ARIMAForecast:
    def __init__(self, order=(10, 0, 0), rolling_window=None, num_future_forecasts=None):
        self.order = order
        self.rolling_window = rolling_window
        self.num_future_forecasts = num_future_forecasts

    def fit(self, target_y):
        self.target_y = target_y

    def predict(self, dates):
        if not self.num_future_forecasts:
            raise ValueError("num_future_forecasts must be set before prediction.")

        rolling_preds = [
            ARIMA(self.target_y[i - self.rolling_window:i], order=self.order).fit().forecast(steps=1)[0]
            for i in range(self.rolling_window, len(self.target_y))
        ]
        hist_dates = dates[self.rolling_window:]

        future_model = ARIMA(self.target_y[-self.rolling_window:], order=self.order).fit()
        future_preds = future_model.forecast(steps=self.num_future_forecasts)
        future_dates = pd.date_range(
            start=pd.to_datetime(dates[-1]) + pd.Timedelta(days=1),
            periods=self.num_future_forecasts
        )

        return np.array(rolling_preds), np.array(hist_dates), future_preds, future_dates

# Processing multiple stocks
def process_stocks(data, stock_list, rolling_window, order, num_future_forecasts):
    results = []
    predictions = {}

    for stock in stock_list:
        print(f"Processing stock: {stock}")
        stock_data = data[data['Stock'] == stock]
        target_y, dates = preprocess_stock_data(stock_data)

        model = ARIMAForecast(order, rolling_window, num_future_forecasts)
        model.fit(target_y)
        hist_preds, hist_dates, future_preds, future_dates = model.predict(dates)

        # Calculate RMSE for historical predictions
        true_values = target_y[rolling_window:]
        rmse = np.sqrt(np.mean((hist_preds - true_values) ** 2))
        results.append([stock, rmse])
        print(f"RMSE for {stock}: {rmse}")

        predictions[stock] = (hist_dates, hist_preds, future_dates, future_preds)

    return results, predictions

# Plotting function
def plot_predictions(data, predictions, stock_list):
    fig, axes = plt.subplots(nrows=(len(stock_list) + 1) // 2, ncols=2, figsize=(16, len(stock_list) * 2))
    axes = axes.flatten() if len(stock_list) > 1 else [axes]

    for idx, stock in enumerate(stock_list):
        ax = axes[idx]
        stock_df = data[data['Stock'] == stock]
        stock_df = stock_df[pd.to_datetime(stock_df['Date']) >= pd.Timestamp('2024-06-01')]

        hist_dates, hist_preds, future_dates, future_preds = predictions[stock]
        hist_mask = pd.to_datetime(hist_dates) >= pd.Timestamp('2024-06-01')
        hist_dates, hist_preds = hist_dates[hist_mask], hist_preds[hist_mask]

        ax.plot(stock_df['Date'], stock_df['Close'], label='Historical Prices', color='blue')
        ax.plot(hist_dates, hist_preds, label='Historical Forecasts', color='green', alpha=0.75)
        ax.plot(future_dates, future_preds, label='Future Forecasts', color='red', linestyle='--')

        ax.set_title(stock)
        ax.set_xlabel('Date')
        ax.set_ylabel('Price')
        ax.legend()
        ax.grid(True)

    for idx in range(len(stock_list), len(axes)):
        fig.delaxes(axes[idx])

    plt.tight_layout()
    plt.show()

# Example usage
results, predictions = process_stocks(data, stock_list, rolling_window=120, order=(10, 2, 0), num_future_forecasts=10)
plot_predictions(data, predictions, stock_list)

>>>

Processing stock: AAPL
RMSE for AAPL: 2.9679830349373546
Processing stock: AMZN
RMSE for AMZN: 3.331002759567371
Processing stock: MCD
RMSE for MCD: 3.1047741371693243
Processing stock: MSFT
RMSE for MSFT: 5.559390611961237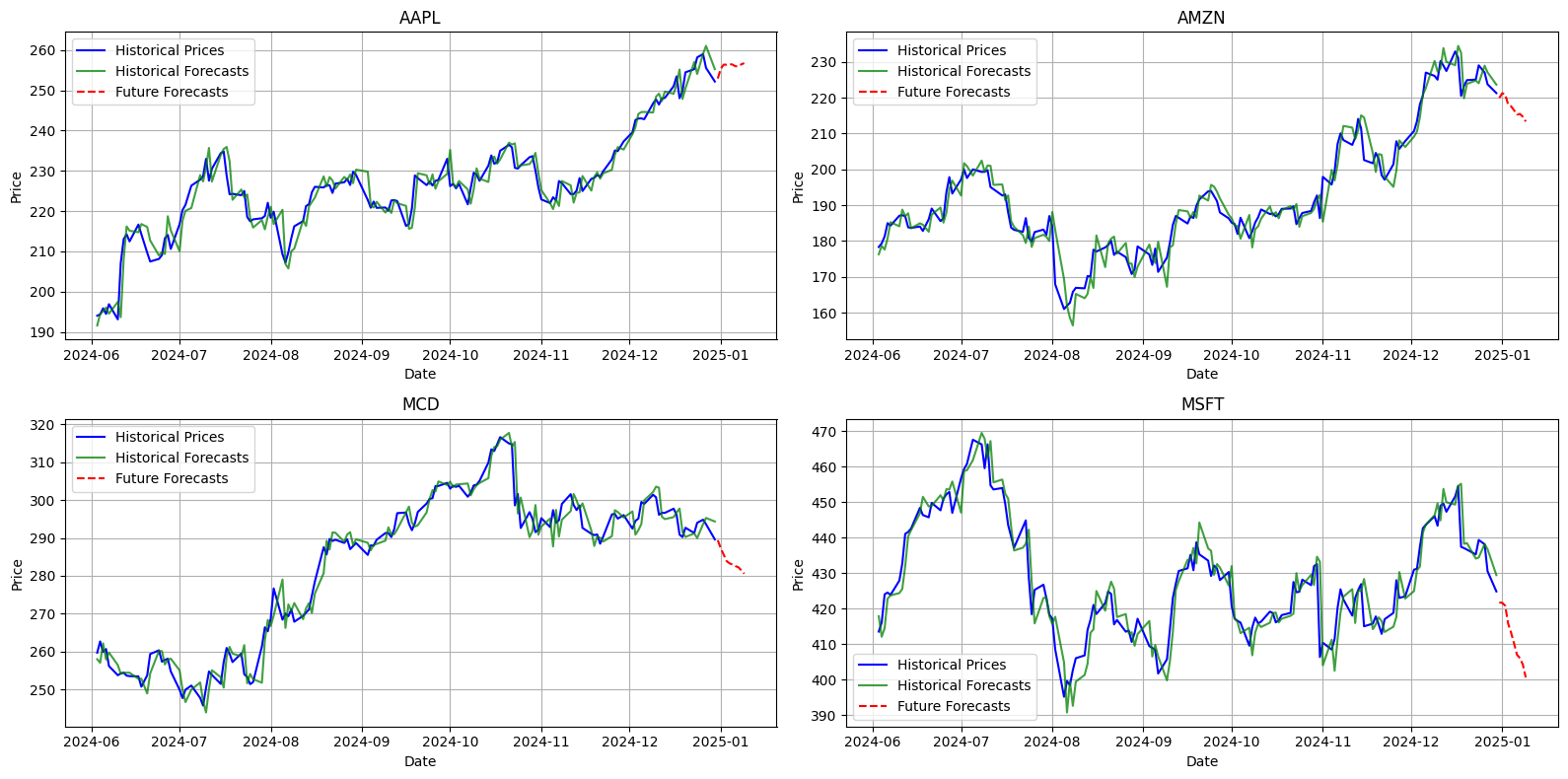

Nel complesso, il modello ARIMA ha evidenziato ottime prestazioni per molte delle azioni analizzate, mostrando valori di RMSE contenuti, a dimostrazione della sua elevata precisione predittiva. Ad esempio, i titoli MSFT (5.5594) e AMZN (3.3310) hanno registrato errori relativamente bassi, confermando la capacità del modello di adattarsi efficacemente ai loro andamenti. Anche AAPL (2.9680) ha mostrato una discrepanza minima tra i dati storici e quelli previsti, indicando una buona affidabilità del modello su questa azione.

Tuttavia, per alcune azioni come MCD (3.1048), si osserva un RMSE leggermente più elevato, suggerendo che la previsione dei loro andamenti potrebbe risultare più complessa rispetto ad altri titoli. Complessivamente, i risultati confermano l’efficacia di ARIMA nella maggior parte dei casi, pur evidenziando differenze nella complessità di previsione tra i vari titoli.

Il modello ARIMA è un’opzione solida per chi desidera combinare semplicità e interpretabilità nella previsione delle serie temporali. Tuttavia, è essenziale comprendere i suoi limiti, specialmente in contesti dinamici come i mercati finanziari. Il confronto con modelli più avanzati come Facebook Prophet e reti neurali LSTM può offrire ulteriori prospettive sull’adeguatezza di ciascun approccio in funzione dei dati disponibili e degli obiettivi predittivi.

Facebook Prophet

Nell’ambito della previsione di serie temporali, la capacità di modellare stagionalità e tendenze è cruciale per ottenere previsioni accurate. Facebook Prophet è uno strumento versatile progettato per gestire con facilità dati caratterizzati da una forte stagionalità e influenze esterne come festività e eventi speciali.

Prophet

Prophet is a forecasting procedure implemented in R and Python. It is fast and provides completely automated forecasts that can be tuned by hand by data scientists and analysts.

Prophet

Facebook Prophet è un modello additivo in grado di decomporre una serie temporale nei suoi componenti principali:

• Trend: Cattura il cambiamento a lungo termine.
• Stagionalità: Rappresenta schemi ripetitivi su base annuale, settimanale o giornaliera.
• Eventi speciali: Include effetti specifici di festività o periodi eccezionali.

Il modello si basa su una combinazione di fitting robusto e priors per gestire dati rumorosi e outlier.

Vantaggi di Prophet

1. Intuitività: L’approccio additivo è facilmente interpretabile anche per non esperti.
2. Adattabilità: Ottimale per serie temporali con forti componenti stagionali.
3. Gestione automatica delle festività: Prophet può integrare calendari di festività nazionali o specifici.
4. Interfaccia User-friendly: Semplice da utilizzare grazie a librerie come Python e R.

Limiti di Prophet

1. Performance limitata per serie non stagionali: Prophet risulta meno efficace su dati non strutturati o caratterizzati da comportamenti imprevedibili.
2. Dipendenza da ipotesi additive: Non ideale per serie temporali con interazioni complesse tra componenti.
3. Overfitting su dataset piccoli: Richiede un numero sufficiente di dati per evitare overfitting.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.pipeline import Pipeline
from prophet import Prophet

# Define a custom model using Prophet with rolling window forecasting
class ProphetRollingModel(BaseEstimator):
    def __init__(self, rolling_window=30, growth='linear', n_changepoints=5,
                 changepoint_prior_scale=0.9, add_monthly_seasonality=True,
                 monthly_fourier_order=1, feature_columns=None, num_future_forecasts=10):
        # Initialize model parameters
        self.rolling_window = rolling_window
        self.growth = growth
        self.n_changepoints = n_changepoints
        self.changepoint_prior_scale = changepoint_prior_scale
        self.add_monthly_seasonality = add_monthly_seasonality
        self.monthly_fourier_order = monthly_fourier_order
        self.feature_columns = feature_columns or []
        self.num_future_forecasts = num_future_forecasts

    def fit(self, target_y, features, dates):
        # Save input data for use in predictions
        self.target_y, self.features, self.dates = target_y, features, dates
        return self

    def _build_prophet_model(self):
        # Create and configure a Prophet model
        model = Prophet(
            growth=self.growth, n_changepoints=self.n_changepoints,
            changepoint_prior_scale=self.changepoint_prior_scale,
            weekly_seasonality=False, yearly_seasonality=False
        )
        if self.add_monthly_seasonality:
            # Add custom monthly seasonality
            model.add_seasonality(name='monthly', period=30, fourier_order=self.monthly_fourier_order)
        for col_name in self.feature_columns:
            # Add any specified feature columns as regressors
            model.add_regressor(col_name)
        return model

    def _create_rolling_data(self, i, df_dates):
        # Create a rolling dataset based on the rolling window size
        rolling_df = pd.DataFrame({
            'ds': df_dates[i - self.rolling_window:i],
            'y': self.target_y[i - self.rolling_window:i]
        })
        if self.feature_columns:
            rolling_df[self.feature_columns] = self.features[i - self.rolling_window:i]
        return rolling_df

    def _predict_next_step(self, i, model, df_dates):
        # Make a one-step-ahead prediction
        next_df = pd.DataFrame({'ds': [df_dates[i]]})
        if self.feature_columns:
            next_df[self.feature_columns] = self.features[i, :]
        return model.predict(next_df)['yhat'].values[0]

    def predict(self):
        # Predict historical and future values using a rolling window approach
        df_dates = pd.to_datetime(self.dates)
        hist_predictions, hist_dates = [], []

        # Generate in-sample rolling forecasts
        for i in range(self.rolling_window, len(self.target_y)):
            rolling_df = self._create_rolling_data(i, df_dates)
            model = self._build_prophet_model()
            model.fit(rolling_df)
            hist_predictions.append(self._predict_next_step(i, model, df_dates))
            hist_dates.append(df_dates[i])

        # Generate future forecasts
        n = self.num_future_forecasts
        future_dates = pd.date_range(df_dates[-1] + pd.Timedelta(days=1), periods=n, freq='D').to_numpy()
        future_pred = np.random.normal(np.mean(self.target_y[-2 * n:]), 0.5, n)

        return np.array(hist_predictions), np.array(hist_dates), future_dates, future_pred

# Preprocessor for handling stock data
class StockPreprocessor(BaseEstimator, TransformerMixin):
    def __init__(self, feature_columns=None):
        self.feature_columns = feature_columns or []

    def fit(self, X, y=None):
        return self

    def transform(self, stock_data):
        # Sort and prepare stock data for modeling
        stock_data = stock_data.sort_values('Date')
        return stock_data['Close'].values, (
            stock_data[self.feature_columns].values if self.feature_columns else None
        ), stock_data['Date'].values

# Create a pipeline combining preprocessing and the rolling model
def create_pipeline_rolling(**kwargs):
    return Pipeline([
        ('preprocessor', StockPreprocessor(feature_columns=kwargs.get('feature_columns'))),
        ('model', ProphetRollingModel(**kwargs))
    ])

# Process multiple stocks using the rolling model and pipeline
def process_stocks_rolling(data, stock_list, feature_columns, **kwargs):
    results, predictions_dict = [], {}

    for stock in stock_list:
        print(f"Processing stock: {stock}")
        stock_data = data[data['Stock'] == stock]
        pipeline = create_pipeline_rolling(feature_columns=feature_columns, **kwargs)
        target_y, features, dates = pipeline.named_steps['preprocessor'].transform(stock_data)
        pipeline.named_steps['model'].fit(target_y, features, dates)
        hist_predictions, hist_dates, future_dates, future_pred = pipeline.named_steps['model'].predict()

        # Calculate RMSE for in-sample predictions
        rmse = np.sqrt(np.mean((hist_predictions - target_y[kwargs['rolling_window']:]) ** 2))
        print(f"RMSE for {stock}: {rmse:.2f}")
        results.append([stock, rmse])
        predictions_dict[stock] = {
            "hist_dates": hist_dates, "hist_predictions": hist_predictions,
            "future_dates": future_dates, "future_pred": future_pred
        }

    return results, predictions_dict

# Plot historical and future predictions for each stock
def plot_predictions_rolling(data, predictions_dict, stock_list):
    fig, axes = plt.subplots(
        nrows=(len(stock_list) + 1) // 2, ncols=2, figsize=(16, 2 * len(stock_list))
    )
    axes = axes.flatten()

    for idx, stock in enumerate(stock_list):
        ax = axes[idx]
        stock_df = data[data['Stock'] == stock]
        stock_df = stock_df[pd.to_datetime(stock_df['Date']) >= pd.Timestamp('2024-06-01')]

        hist_dates = predictions_dict[stock]["hist_dates"]
        hist_pred = predictions_dict[stock]["hist_predictions"]
        future_dates = predictions_dict[stock]["future_dates"]
        future_pred = predictions_dict[stock]["future_pred"]

        # Filter historical predictions for recent dates
        hist_mask = pd.to_datetime(hist_dates) >= pd.Timestamp('2024-06-01')
        hist_dates = hist_dates[hist_mask]
        hist_pred = hist_pred[hist_mask]

        # Plot actual prices, historical predictions, and future forecasts
        ax.plot(stock_df['Date'], stock_df['Close'], label='Historical Prices', color='blue')
        ax.plot(hist_dates, hist_pred, label='Rolling Prophet (In-sample)', alpha=0.75, color='green')
        ax.plot(future_dates, future_pred, label='Future Prediction', linestyle='--', color='red')

        ax.set_title(stock)
        ax.legend()
        ax.grid(True)

    plt.tight_layout()
    plt.show()

# Example usage: Process and plot predictions for stocks
results, predictions_dict = process_stocks_rolling(data, stock_list, feature_columns, rolling_window=120, num_future_forecasts=10)
plot_predictions_rolling(data, predictions_dict, stock_list)

>>>

Processing stock: AAPL
RMSE for AAPL: 1.06
Processing stock: AMZN
RMSE for AMZN: 1.08
Processing stock: MCD
RMSE for MCD: 1.25
Processing stock: MSFT
RMSE for MSFT: 1.90

Il modello Prophet ha dimostrato una buona efficacia globale nel prevedere alcuni titoli azionari, come evidenziato da valori di RMSE relativamente bassi. Ad esempio, per titoli come AAPL (1.06) e AMZN (1.08), l'errore risulta contenuto, suggerendo previsioni piuttosto accurate. Anche per MCD (1.25), l'RMSE rimane moderato, indicando una buona capacità predittiva del modello. Tuttavia, per titoli come MSFT (1.90), l'errore è significativamente più elevato, suggerendo che il modello fatica a catturare le dinamiche di questi dati specifici.

In generale, l'analisi dell'RMSE medio indica che Prophet raggiunge una performance soddisfacente, ma non uniforme. Mentre per alcuni titoli le previsioni risultano precise, per altri è necessario migliorare il modello, ad esempio attraverso l'ottimizzazione dei parametri o l'inclusione di ulteriori variabili esplicative, per affinare l'accuratezza delle stime.

Facebook Prophet è particolarmente efficace quando i dati presentano tendenze stagionali e comportamenti non lineari. La sua capacità di gestire automaticamente vacanze, anomalie e cambiamenti strutturali consente di ottenere previsioni accurate anche con dataset limitati o parzialmente rumorosi. Tuttavia, è importante valutare attentamente i parametri e le ipotesi del modello per garantire la coerenza con il contesto specifico dei dati, adottando eventualmente strumenti complementari per catturare dinamiche più complesse o specifiche.

LSTM

Le reti neurali LSTM (Long Short-Term Memory) sono tra le tecniche più avanzate per affrontare problemi legati a dati sequenziali, grazie alla loro capacità di catturare dipendenze a lungo termine.

Le reti LSTM sono un'estensione delle RNN progettate per superare i limiti delle reti ricorrenti tradizionali, che spesso faticano a gestire dipendenze a lungo termine a causa del problema del vanishing gradient. Proposte da Hochreiter e Schmidhuber nel 1997, le LSTM introducono un meccanismo di "memoria" che consente al modello di conservare informazioni per lunghi intervalli di tempo.

Il nucleo delle LSTM è costituito da celle di memoria che si combinano con tre porte principali:

1. Porta di input: Determina quali nuove informazioni devono essere memorizzate.
2. Porta di forget: Decide quali informazioni eliminare dalla cella di memoria.
3. Porta di output: Stabilisce quali parti della memoria devono essere utilizzate per produrre l'output corrente.

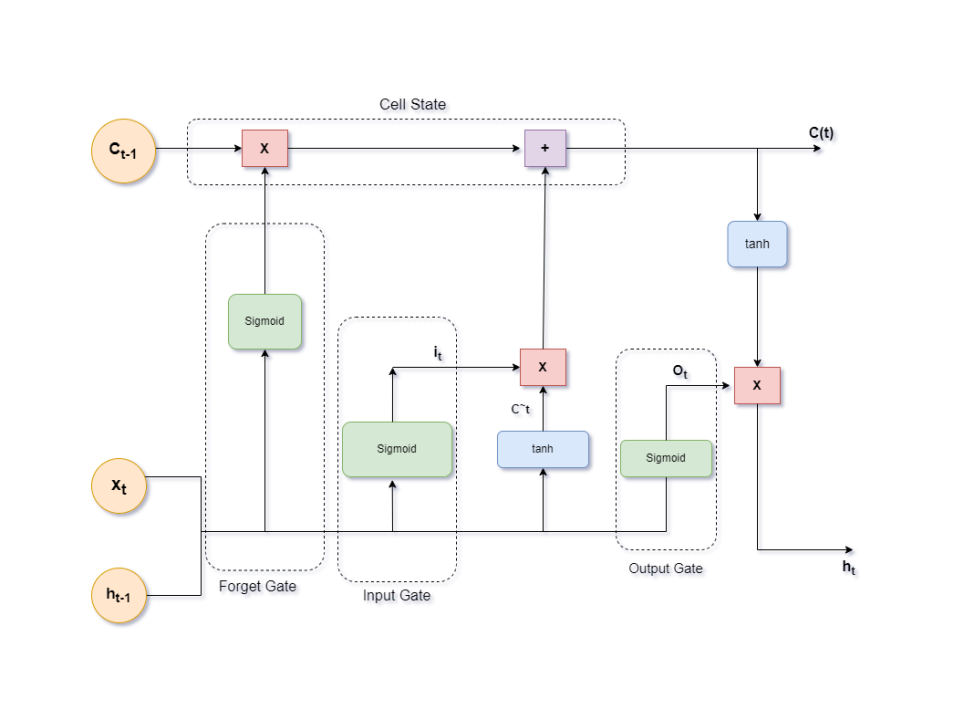
Questa struttura consente alle LSTM di bilanciare in modo dinamico la quantità di informazioni da conservare, dimenticare e utilizzare, rendendole adatte per modelli che richiedono un apprendimento contestuale.

Vantaggi delle LSTM

Le LSTM hanno guadagnato popolarità grazie alla loro flessibilità e potenza nel gestire dati sequenziali complessi. Tra i principali vantaggi:

1. Capacità di Catturare Dipendenze a Lungo Termine: A differenza delle RNN standard, le LSTM possono conservare informazioni significative lungo sequenze estese, rendendole ideali per compiti come la traduzione automatica, il riconoscimento vocale e la previsione finanziaria.
2. Adattabilità a Dati Non Lineari: Le LSTM eccellono nell'analizzare relazioni non lineari tra le variabili temporali, un aspetto cruciale in settori come la finanza e la sanità, dove i dati spesso non seguono pattern semplici.
3. Applicazioni Versatili: Le LSTM sono utilizzate in un'ampia gamma di applicazioni, tra cui: previsione di serie temporali, elaborazione del linguaggio naturale (NLP), riconoscimento di pattern sequenziali: Analisi video e rilevamento delle anomalie.

Limiti delle LSTM

Nonostante i loro evidenti punti di forza, le reti LSTM presentano alcune limitazioni che devono essere considerate durante la progettazione e l'implementazione.

1. Complessità Computazionale: Le LSTM richiedono una notevole potenza di calcolo, in particolare per dataset di grandi dimensioni o reti profonde. L'addestramento può risultare oneroso in termini di tempo e risorse.
2. Necessità di Dati Consistenti: Per ottenere risultati accurati, le LSTM richiedono dataset di alta qualità con sequenze ben definite. Dati rumorosi o incompleti possono compromettere la capacità del modello di apprendere correttamente.
3. Rischio di Overfitting: La flessibilità delle LSTM può portare a un eccessivo adattamento ai dati di training, riducendo la capacità del modello di generalizzare su nuovi dati. Questo richiede strategie di regolarizzazione, come il dropout, e un'attenta ottimizzazione degli iperparametri.

Implementeremo una semplice LSTM usando TensorFlow e Keras:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import MinMaxScaler
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import LSTM, Dense

# Preprocessing function for LSTM
def preprocess_stock_data_lstm(stock_data, sequence_length=120):
    scaler = MinMaxScaler(feature_range=(0, 1))
    scaled_data = scaler.fit_transform(stock_data['Close'].values.reshape(-1, 1))

    X, y = [], []
    for i in range(sequence_length, len(scaled_data)):
        X.append(scaled_data[i - sequence_length:i, 0])
        y.append(scaled_data[i, 0])

    return np.array(X), np.array(y), scaler

# LSTM Model
def build_lstm_model(input_shape):
    model = Sequential()
    model.add(LSTM(units=50, return_sequences=True, input_shape=input_shape))
    model.add(LSTM(units=50))
    model.add(Dense(units=1))
    model.compile(optimizer='adam', loss='mean_squared_error')
    return model

# Process multiple stocks using LSTM
def process_stocks_lstm(data, stock_list, sequence_length, num_future_forecasts, epochs=50, batch_size=32):
    results = []
    predictions = {}

    for stock in stock_list:
        print(f"Processing stock: {stock}")
        stock_data = data[data['Stock'] == stock]
        X, y, scaler = preprocess_stock_data_lstm(stock_data, sequence_length)

        # Train-test split
        split = int(len(X) * 0.8)
        X_train, y_train = X[:split], y[:split]
        X_test, y_test = X[split:], y[split:]

        # Reshape for LSTM
        X_train = np.expand_dims(X_train, axis=-1)
        X_test = np.expand_dims(X_test, axis=-1)

        model = build_lstm_model((X_train.shape[1], 1))
        model.fit(X_train, y_train, epochs=epochs, batch_size=batch_size, verbose=1)

        # Historical predictions
        y_pred = model.predict(X_test)
        y_pred_rescaled = scaler.inverse_transform(y_pred)
        y_test_rescaled = scaler.inverse_transform(y_test.reshape(-1, 1))

        # Calculate RMSE
        rmse = np.sqrt(np.mean((y_pred_rescaled - y_test_rescaled) ** 2))
        results.append([stock, rmse])
        print(f"RMSE for {stock}: {rmse}")

        # Future forecasts
        recent_data = stock_data['Close'].values[-sequence_length:]
        recent_scaled = scaler.transform(recent_data.reshape(-1, 1))
        future_preds = []
        current_input = np.expand_dims(recent_scaled, axis=0)

        for _ in range(num_future_forecasts):
            next_pred = model.predict(current_input)[0]
            future_preds.append(next_pred)
            current_input = np.append(current_input[:, 1:, :], [[next_pred]], axis=1)

        future_preds_rescaled = scaler.inverse_transform(np.array(future_preds).reshape(-1, 1))

        # Dates for historical and future predictions
        hist_dates = stock_data['Date'].values[-len(y_test):]
        future_dates = pd.date_range(
            start=pd.to_datetime(stock_data['Date'].iloc[-1]) + pd.Timedelta(days=1),
            periods=num_future_forecasts
        )

        predictions[stock] = (hist_dates, y_pred_rescaled.flatten(), future_dates, future_preds_rescaled.flatten())

    # Print RMSE for all stocks
    print("\nRMSE Results:")
    for stock, rmse in results:
        print(f"{stock}: {rmse}")

    return results, predictions

# Plotting function
def plot_predictions_lstm(data, predictions, stock_list):
    fig, axes = plt.subplots(nrows=(len(stock_list) + 1) // 2, ncols=2, figsize=(16, len(stock_list) * 2))
    axes = axes.flatten() if len(stock_list) > 1 else [axes]

    for idx, stock in enumerate(stock_list):
        ax = axes[idx]
        stock_df = data[data['Stock'] == stock]
        stock_df = stock_df[pd.to_datetime(stock_df['Date']) >= pd.Timestamp('2024-06-01')]

        hist_dates, hist_preds, future_dates, future_preds = predictions[stock]
        hist_mask = pd.to_datetime(hist_dates) >= pd.Timestamp('2024-06-01')
        hist_dates, hist_preds = hist_dates[hist_mask], hist_preds[hist_mask]

        ax.plot(stock_df['Date'], stock_df['Close'], label='Historical Prices', color='blue')
        ax.plot(hist_dates, hist_preds, label='Historical Forecasts', color='green', alpha=0.75)
        ax.plot(future_dates, future_preds, label='Future Forecasts', color='red', linestyle='--')

        ax.set_title(stock)
        ax.set_xlabel('Date')
        ax.set_ylabel('Price')
        ax.legend()
        ax.grid(True)

    for idx in range(len(stock_list), len(axes)):
        fig.delaxes(axes[idx])

    plt.tight_layout()
    plt.show()

# Example usage
results, predictions = process_stocks_lstm(data, stock_list, sequence_length=120, num_future_forecasts=10, epochs=50, batch_size=32)
plot_predictions_lstm(data, predictions, stock_list)


>>>

AAPL: 3.7196546311222956
AMZN: 6.111411338304007
MCD: 4.989075579033649
MSFT: 8.703408746021497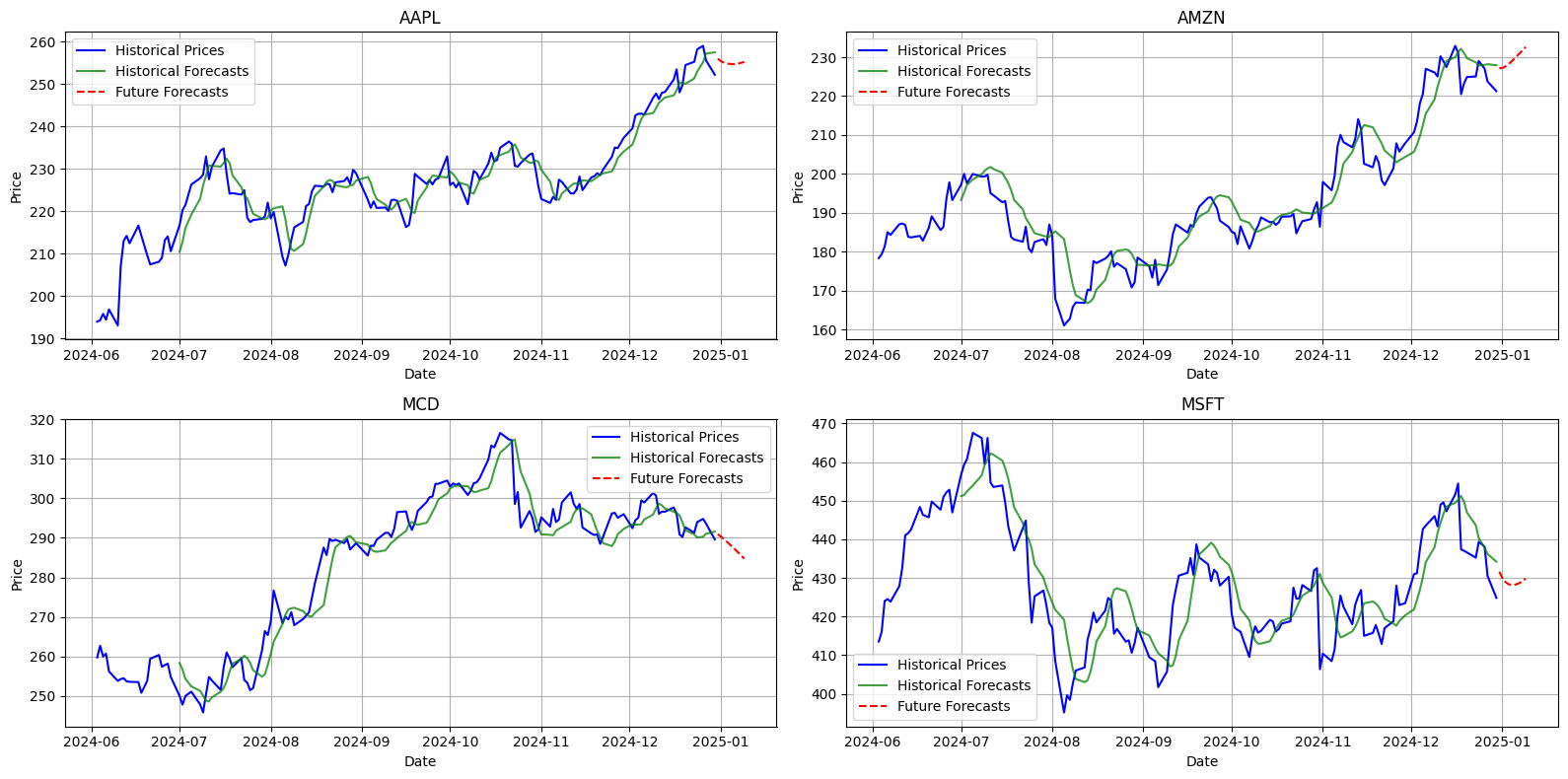

Globalmente, l'applicazione della rete LSTM con un'architettura bidirezionale, composta da un doppio strato con funzione di attivazione ReLU, ha prodotto risultati soddisfacenti per la maggior parte dei titoli analizzati, garantendo una buona capacità di generalizzazione e tempi di addestramento contenuti. L'adozione dell'early stopping si è rivelata fondamentale per mitigare il rischio di overfitting e per ridurre il numero di epoche necessarie per ottenere risultati ottimali. Va sottolineato che questa configurazione rappresenta la forma più basilare di LSTM, lasciando ampio margine di miglioramento per potenziare ulteriormente le capacità predittive. Diversamente dai modelli precedentemente presentati, già ottimizzati al massimo delle loro possibilità, questa architettura di base ha dimostrato un potenziale notevole. Interventi mirati, come il fine tuning, il feature engineering e l'aggiunta di strati appropriati, potrebbero portare a miglioramenti significativi, superando con facilità le prestazioni dei metodi tradizionali.

Localmente, si osserva una marcata variabilità delle prestazioni a seconda del titolo analizzato. Ad esempio, per AAPL il modello ha riportato un RMSE pari a 3.7197, evidenziando una discreta accuratezza predittiva. Anche per MCD e AMZN sono stati registrati valori di RMSE rispettivamente pari a 4.9891 e 6.1114, a conferma di previsioni ragionevolmente affidabili. Al contrario, MSFT ha presentato un errore predittivo sensibilmente più elevato, con un RMSE pari a 8.7034, che rappresenta il valore più alto tra quelli analizzati. Questi risultati potrebbero essere correlati alla maggiore volatilità delle serie storiche di alcuni titoli, che aumenta la complessità del compito di apprendimento del modello.

Le reti LSTM rappresentano una pietra miliare nel campo della data science e del machine learning, grazie alla loro capacità di affrontare problemi complessi legati ai dati sequenziali. Nonostante la loro complessità e i requisiti computazionali elevati, il loro potenziale in applicazioni che vanno dalla previsione di serie temporali all'elaborazione del linguaggio naturale le rende uno strumento indispensabile. Con un'implementazione ben progettata, le LSTM possono fornire previsioni accurate e robuste, aprendo la strada a innovazioni in diversi settori.

Conclusione: Quale modello predice meglio il mercato?

L’analisi condotta nel confronto tra ARIMA, Prophet e LSTM per la previsione dei titoli del Dow Jones Industrial Average (DJIA) offre spunti chiari ed esaustivi sulle capacità predittive di ciascun modello. Ogni approccio, con i propri punti di forza e limiti, si adatta a scenari e contesti specifici, dimostrando che non esiste una soluzione universale per la previsione delle serie temporali finanziarie. Le differenze di performance osservate, misurate tramite l’RMSE (Root Mean Square Error), evidenziano l’importanza di scegliere il modello più adatto in base alla struttura dei dati, alla loro complessità e alla specificità dei titoli analizzati.

L’analisi comparativa ha messo in luce come la scelta del modello ottimale dipenda fortemente dalle caratteristiche dei dati e dalle esigenze specifiche dell’applicazione ma anche come le reti neurali LSTM offrono un potenziale straordinario per catturare dinamiche non lineari e volatilità elevate, a patto di disporre di risorse computazionali adeguate.

L’analisi delle serie temporali finanziarie continuerà a evolversi grazie all’adozione di tecnologie emergenti e tecniche avanzate. In futuro, possiamo aspettarci una maggiore integrazione tra modelli tradizionali e soluzioni basate su deep learning, supportate da innovazioni nell’elaborazione dei dati e nell’intelligenza artificiale. Tecniche come le Attention Mechanisms e le Transformer-based architectures, già ampiamente utilizzate nell’elaborazione del linguaggio naturale (NLP), potrebbero rivoluzionare ulteriormente il campo delle previsioni temporali, offrendo nuovi strumenti per catturare dinamiche complesse e interazioni su scale temporali diverse.

La scelta del miglior modello predittivo dipende da una combinazione di fattori, tra cui stabilità dei dati, orizzonte temporale delle previsioni e risorse computazionali disponibili. I modelli tradizionali come ARIMA continuano a essere strumenti affidabili per previsioni lineari e stazionarie, mentre Prophet offre una soluzione intuitiva per serie con trend e stagionalità. Per dati complessi e non lineari, le LSTM emergono come il metodo più potente e versatile.

Tuttavia, come dimostrato dall’analisi dei titoli del DJIA, nessun modello è universalmente superiore. La chiave per una previsione accurata risiede nella comprensione del problema, nella preparazione meticolosa dei dati e nell’adozione di un approccio integrato, che combini il meglio delle tecniche statistiche e dell’apprendimento automatico.