Se sei un analista, indipendentemente dal tuo settore lavorativo, sei sicuramente consapevole che esistono molti approcci diversi per la previsione del mercato azionario. I più rilevanti oggi utilizzano principalmente reti neurali applicate a dati in sequenza, come LSTM, o coinvolgono l'analisi del sentiment e la signal detection.
Questi approcci sono decisamente interessanti e per una buona ragione: ci sono molte risorse su Internet che trattano gli argomenti menzionati. Questa è una ottima cosa, poiché gli possiamo avviare i nostri progetti seguendo una linea di base condivisa e poi espanderli con le proprie metodologie.
Oggi voglio proporre un approccio diverso, quello che ho letteralmente sognato un paio di settimane fa e che mi ha fatto riflettere per le possibili opportunità. Sto parlando del clustering di serie temporali applicato ai mercati azionari.
Il mio pensiero principale è stato
E se potessi identificare pattern nei dati, trovare quelli simili, raggrupparli insieme e assegnare opportunità di investimento a ciascuno di essi?
Questo mi permetterebbe di individuare sequenze rilevanti che potrebbero prevedere una tendenza specifica verso l'alto o verso il basso.
Ho dedicato alcune ore a questo progetto e vorrei condividere con voi la prima parte di questa serie. Mentre continuo a lavorare su questo progetto, condividerò le mie scoperte in un altro articolo.
Tieni presente che questo è il mio approccio: se ti piace il ragionamento generale ma faresti qualcosa di diverso, fammelo sapere con un commento 👌
Spero che tu sia entusiasta come lo sono io per questo progetto. Iniziamo!
L'intuizione alla base del progetto
L'idea è che se prendiamo una serie temporale, indipendentemente dalla sua natura e contesto (che si tratti di un titolo azionario o altro), possiamo dividerla in sequenze e studiare ogni sequenza in isolamento.
Questo ci permette di fare ipotesi su questi segmenti e confrontarli l'uno contro l'altro.
In tal proposito, questa è l'ipotesi per questo problema
Se divido una serie temporale in sequenze di egual misura, posso dividere i tali sequenze in due parti, che chiamerò A e B. B quindi seguirà sempre A.
Studiando A, sono in grado di trovare dei pattern in comune e raggruppare tali A insieme. Questo, di conseguenza, mi permette di calcolare la probabilità che la B segua un andamento simile dato il segmento che la precede A.
L'approccio probabilistico mi sembra quello più adatto. Vedremo tra poco perché.
In conclusione, voglio trovare sequenze che occorrono con un certo grado di somiglianza nell'intera serie temporale. Voglio raggruppare queste sequenze simili e vedere come si comporta la sequenza che segue in termini di trend, che viene calcolato usando la pendenza.
Ecco un diagramma di come ho immaginato di risolvere questo problema
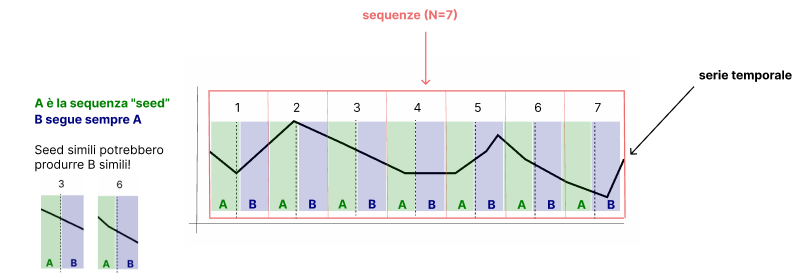
Se scopriamo che alcuni A condividono un alto grado di somiglianza, possiamo raggrupparli insieme e trovare la probabilità che B abbia un trend verso l'alto o verso il basso contando quanti B hanno una pendenza positiva o negativa.
L'algoritmo
Data la spiegazione sopra, ecco come ho progettato l'algoritmo
- Dividere le serie temporali in sequenze di lunghezza N
- Dividere ogni sequenza in due parti in base alla dimensione K per creare sequenze A e B
- Calcolare la somiglianza S tra tutte le sequenze di A
- Raggruppare tutte le sequenze simili di A in base a una soglia
- Per ogni gruppo G calcolare la probabilità P di un trend positivo, negativo o stabile nella sequenza B
- In una nuova serie temporale, identificare una sequenza simile ad una A precedentemente trovata per ottenere la probabilità della successiva porzione B
Se questi passaggi non sono perfettamente chiari, non preoccuparti. Spiegherò ogni passaggio con un'argomentazione dettagliata e con il codice.
Requisiti
Scriveremo la logica da zero in Python, quindi faremo affidamento solo su una manciata di librerie.
# data manipulation
import pandas as pd
import numpy as np
# viz
import matplotlib.pyplot as plt
import seaborn as sns
# time and date libs
import datetime
# stock data access
import pandas_datareader as pdrL'unica menzione che vale la pena fare qui è che useremo pandas_datareader come fornitore di dati del mercato azionario.
La serie temporale
Utilizzeremo pandas_datareader per inserire i dati sulle azioni su Apple di 1000 giorni fa. Ciò includerà 689 punti dati. Questo perché i fine settimana e le altre festività sono escluse.
Non c'è un motivo particolare per cui ho scelto questo numero, sembravano solo dati sufficienti. Definiamo una funzione per reperire i dati
def get_data(ticker: str, start_date: datetime, end_date: datetime) -> pd.DataFrame:
"""
Get stock data input ticker
"""
data = pdr.get_data_yahoo(ticker, start=start_date, end=end_date)
return data
# get 1000 days of data for Apple starting from today
start_date = datetime.datetime.now() - datetime.timedelta(days=1000)
end_date = datetime.datetime.now()
data = get_data('AAPL', start_date=start_date, end_date=end_date)
data.head()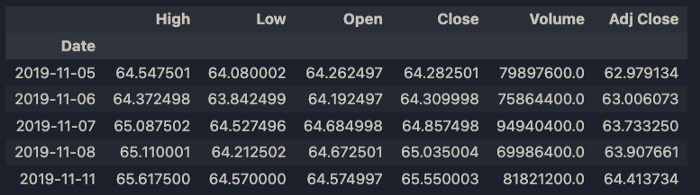
Useremo la colonna di Close come nostra serie temporale.
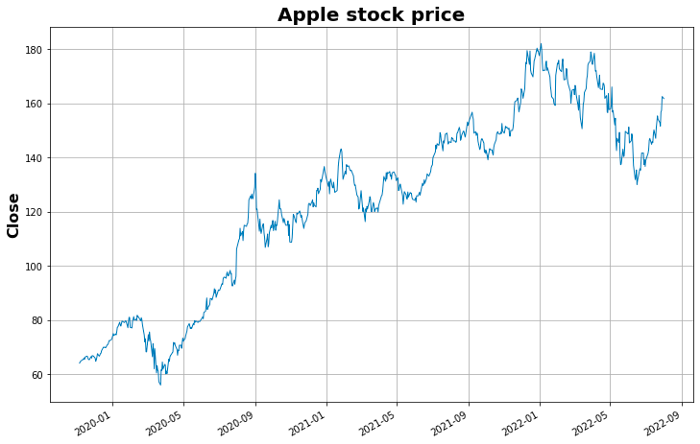
Procediamo ora con la suddivisione della serie temporale secondo la logica sopra citata.
Divisione delle serie temporali
Definiremo due funzioni che divideranno le serie temporali prima in sequenze e poi in sequenze "interne", A e B. Ecco un esempio:
Supponiamo di avere un array Numpy di 20 numeri
s = np.array([i for i in range(30)])
Vogliamo prendere questa serie e dividerla in N segmenti di uguale dimensione. Possiamo raggiungere questo obiettivo in questo modo
def split_time_series(series, n):
"""
Split a time series into n segments of equal size
"""
split_series = [series[i:i+n] for i in range(0, len(series), n)]
# if the last sequence is smaller than n, we discard it
if len(split_series[-1]) < n:
split_series = split_series[:-1]
return np.array(split_series)Se applichiamo questa funzione a s con n = 6 otteniamo una sequenza divisa completa senza elementi scartati (perché non c'è resto quando si divide 30 per 6).

Ora dobbiamo dividere ogni sequenza in due parti in base alla dimensione K per creare sequenze A e B. Definiamo due nuove funzioni chiamate split_sequence e split_sequences per questo.
def split_sequence(sequence, k):
"""
Split a sequence in two, where k is the size of the first sequence
"""
return np.array(sequence[:int(len(sequence) * k)]), np.array(sequence[int(len(sequence) * k):])
def split_sequences(sequences, k=0.80):
"""
Applies split_sequence on all elements of a list or array
"""
return [split_sequence(sequence, k) for sequence in sequences]
view rawIn split_sequence, il parametro K ci permette di controllare la dimensione della prima sequenza. Simile al parametro test_size in train_test_split di Sklearn.
split_sequences invece è solo responsabile dell'applicazione della logica a un array.
Applichiamolo al nostro esempio per capire come funziona
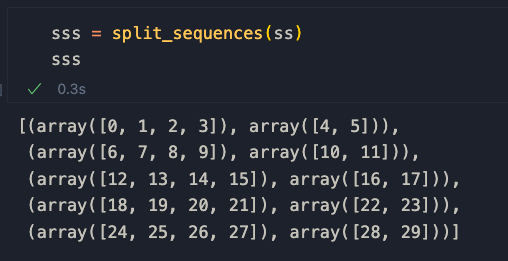
Le sequenze A e B sono definite così
[seq[0] per seq in sss], [seq[1] per seq in sss]
quindi gli elementi accoppiati dal primo e dal secondo elenco nell'array Numpy.
Applichiamo tutto questo alle nostre serie temporali.
N = 15 # window size --> possiamo modificare questo parametro per sperimentare
K = 0.70 # split size --> 70% dei dati è in A, 30% in B
SEQS = split_time_series(list(data['Close'].values), N) # crea sequenze di lunghezza N
SPLIT_SEQS = split_sequences(SEQS, K) # divide le sequenze in due
A = [seq[0] for seq in SPLIT_SEQS]
B = [seq[1] for seq in SPLIT_SEQS]Se diamo un'occhiata a A[0] e B[0], vediamo la prima parte dei dati di chiusura di Apple, a dimostrazione del fatto che la preelaborazione ha avuto successo.
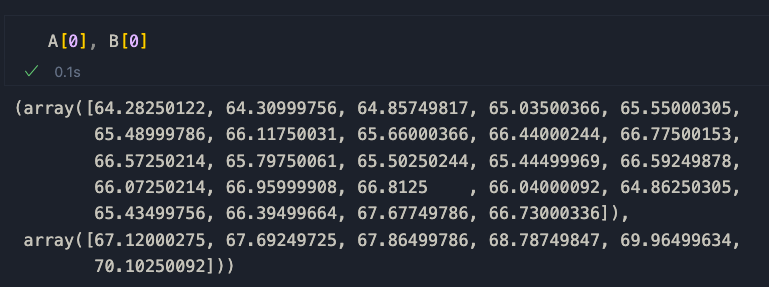
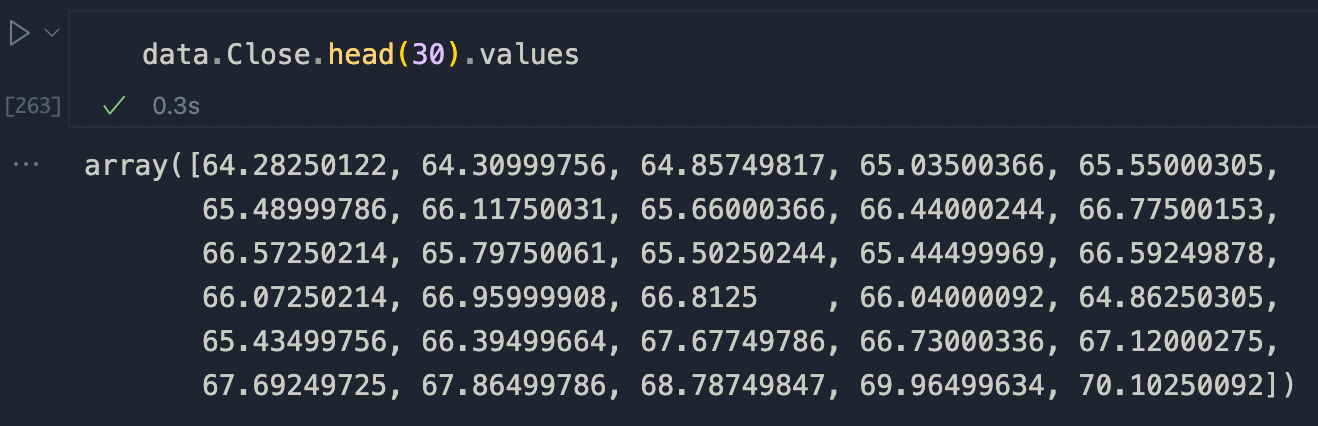
Ora siamo pronti per confrontare le sequenze per similarità.
Calcolo della similarità
Questo è il terzo passaggio dell'algoritmo. Per calcolare la similarità, utilizzeremo una combinazione di correlazione di Pearson e dynamic time warping (distorsione temporale dinamica). La correlazione ci aiuta a far corrispondere la direzione generale delle tendenze, mentre DTW ci aiuta a calcolare la distanza tra i punti. Ci sono molte risorse online su questi due argomenti e ti suggerisco di fare una ricerca più mirata se sei interessato.
La formula è la seguente ed è un prodotto ponderato di correlazione e DWT
\( DWT * (1 — correlation) \)
Anche se forse non ottimale (aiutami a trovare una soluzione migliore!), sembra essere una soluzione funzionale, come vedrai brevemente.
L'idea qui è quella di creare una matrice di similarità S per raccogliere i punteggi per coppie per tutte le sequenze appartenenti ad A. Ricorda che vogliamo trovare elementi simili in A per calcolare la probabilità di trovare una certa B che seguono una certa tendenza.
Gli elementi che condividono una similarità al di sopra di una certa soglia arbitraria verranno raggruppati insieme. Lo vedremo dopo, però. Per ora, scriviamo il codice per il calcolo della similarità.
def compute_correlation(a1, a2):
"""
Calculate the correlation between two vectors
"""
return np.corrcoef(a1, a2)[0, 1]
def compute_dynamic_time_warping(a1, a2):
"""
Compute the dynamic time warping between two sequences
"""
DTW = {}
for i in range(len(a1)):
DTW[(i, -1)] = float('inf')
for i in range(len(a2)):
DTW[(-1, i)] = float('inf')
DTW[(-1, -1)] = 0
for i in range(len(a1)):
for j in range(len(a2)):
dist = (a1[i]-a2[j])**2
DTW[(i, j)] = dist + min(DTW[(i-1, j)], DTW[(i, j-1)], DTW[(i-1, j-1)])
return np.sqrt(DTW[len(a1)-1, len(a2)-1])
# create empty matrix
S = np.zeros((len(A), len(A)))
# populate S
for i in range(len(A)):
for j in range(len(A)):
# weigh the dynamic time warping with the correlation
S[i, j] = compute_dynamic_time_warping(A[i], A[j]) * (1 - compute_correlation(A[i], A[j]))Per chiarezza, stampiamo solo le prime due righe della matrice
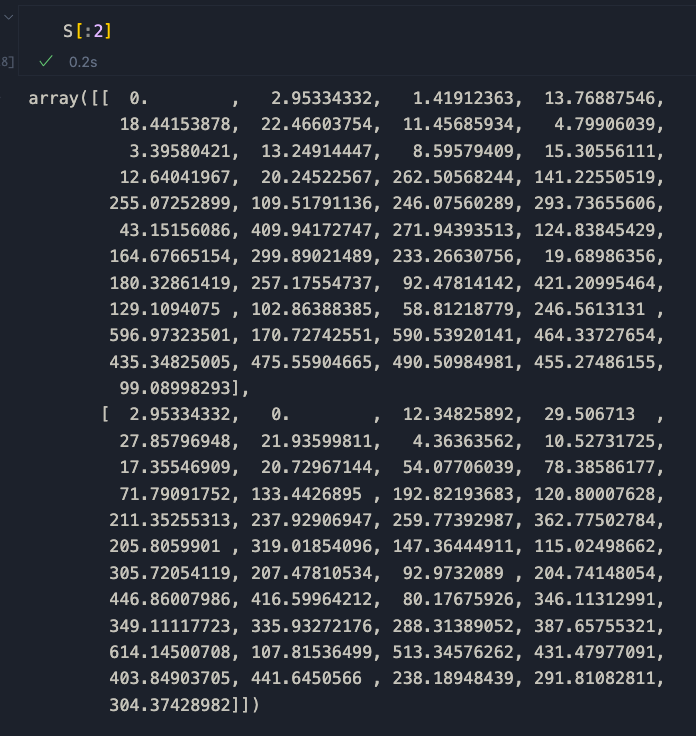
Come possiamo vedere, serie identiche hanno un punteggio di 0. Pertanto, sequenze simili tendono ad avvicinarsi a 0 man mano che diventano sempre più simili. Tracciamo questo con una heatmap.
# plot heatmap of S
fig, ax = plt.subplots(figsize=(20, 10))
sns.heatmap(S, cmap='nipy_spectral_r', square=True, ax=ax)
plt.title("Heatmap of sequence similarities", fontsize=20, fontweight='bold')
plt.xticks(range(len(A)), range(len(A)))
plt.yticks(range(len(A)), range(len(A)))
plt.show()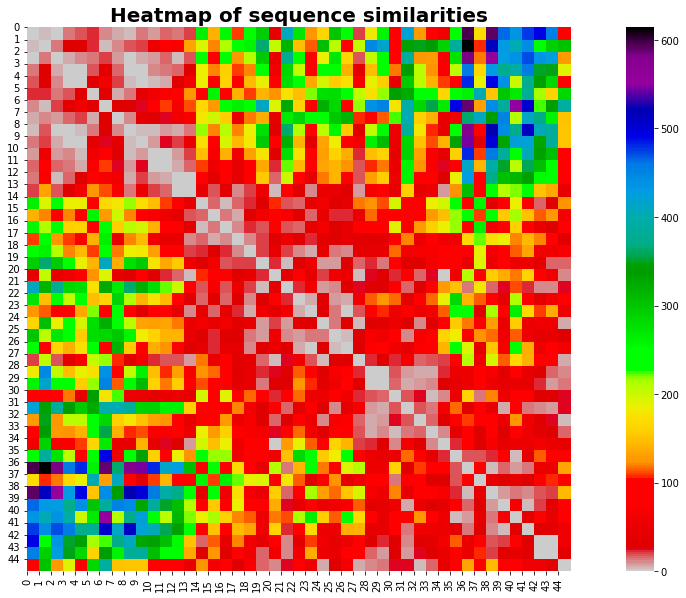
La mappa di calore rivela un'informazione importante: le sequenze più simili si trovano principalmente all'inizio e alla fine della nostra serie temporale.
Non ho idea del perché succeda questa cosa: sarei interessato a sentire i tuoi pensieri al riguardo. Andiamo avanti.
Raggruppamento delle sequenze simili
Il passaggio successivo consiste nel raggruppare insieme sequenze simili in A. L'idea qui è semplice: se le sequenze condividono un punteggio di similarità al di sotto di una certa soglia le raggruppiamo insieme in un dizionario chiamato G. G conterrà tutti i cluster significativi per questo progetto.
# populate G
G = {}
THRESHOLD = 6 # arbitrary value - tweak this to get different results
for i in range(len(S)):
G[i] = []
for j in range(len(S)):
if S[i, j] < THRESHOLD and i != j and (i, j) not in G and (j, i) not in G and j not in G[i]:
G[i].append(j)
# remove any empty groups
G = {k: v for k, v in G.items() if v}Una nota sulla soglia threshold: ho utilizzato il valore di 6 andando per tentativi, poiché sembra produrre i migliori risultati in termini di raggruppamento di similarità (controlla sotto). Potresti voler utilizzare altri valori: sperimenta e fammi sapere come funziona per te.
Vediamo come appare G stampando una parte del dizionario.
Bene ma non benissimo! Un dizionario in realtà non trasmette le informazioni in modo efficace. Vediamo che alcune delle sequenze sono raggruppate insieme, ma che aspetto hanno?
Visualizzazione dei gruppi
E ora la parte più interessante... la visualizzazione dei gruppi!
Per ogni chiave del dizionario G, che si riferisce alla sequenza seed A, tracciamo un grafico dedicato per tutte le sequenze simili al seed.
Ricorda: tutte le sequenze simili condividono un basso valore di distorsione temporale dinamica e una tendenza simile informata dalla correlazione. I parametri utilizzati per ottenere questo raggruppamento sono
N = 15
K = 0.70
THRESHOLD = 6
Creiamo una funzione chiamata plot_similar_sequences che prende in argomento G
import math
def plot_similar_sequences(G):
n_col = round(math.sqrt(len(G)))
if (math.sqrt(len(G)) > int(math.sqrt(len(G)))):
n_col = int(math.sqrt(len(G))) + 1
fig, ax = plt.subplots(n_col, n_col, figsize=(n_col * 20, 20 * n_col))
r = 0
c = 0
for key in G.keys():
for j in G[key]:
if (r >= n_col):
print("Errore")
if (c >= n_col):
c = 0
r = r + 1
ax[r][c].set_title(f'Group {key}', fontdict={"fontsize": 30, "weight": 600})
ax[r][c].plot(A[j], label=j, linestyle='--', linewidth=10, alpha=0.50)
ax[r][c].plot(A[key], label=f'target {j}', linewidth=10, color='black')
ax[r][c].annotate(f'{key}', xy=(len(A[key]) - 1, A[key][-1]), xytext=(len(A[key]) - 1, A[key][-1]))
ax[r][c].plot(np.mean(A[key], axis=0), label='average', color='black', linestyle='--')
c = c + 1
plt.show()Ringrazio Giovanni Moschese per la sua contribuzione nella creazione della funzione per la visualizzazione dei gruppi.
L'output è il seguente
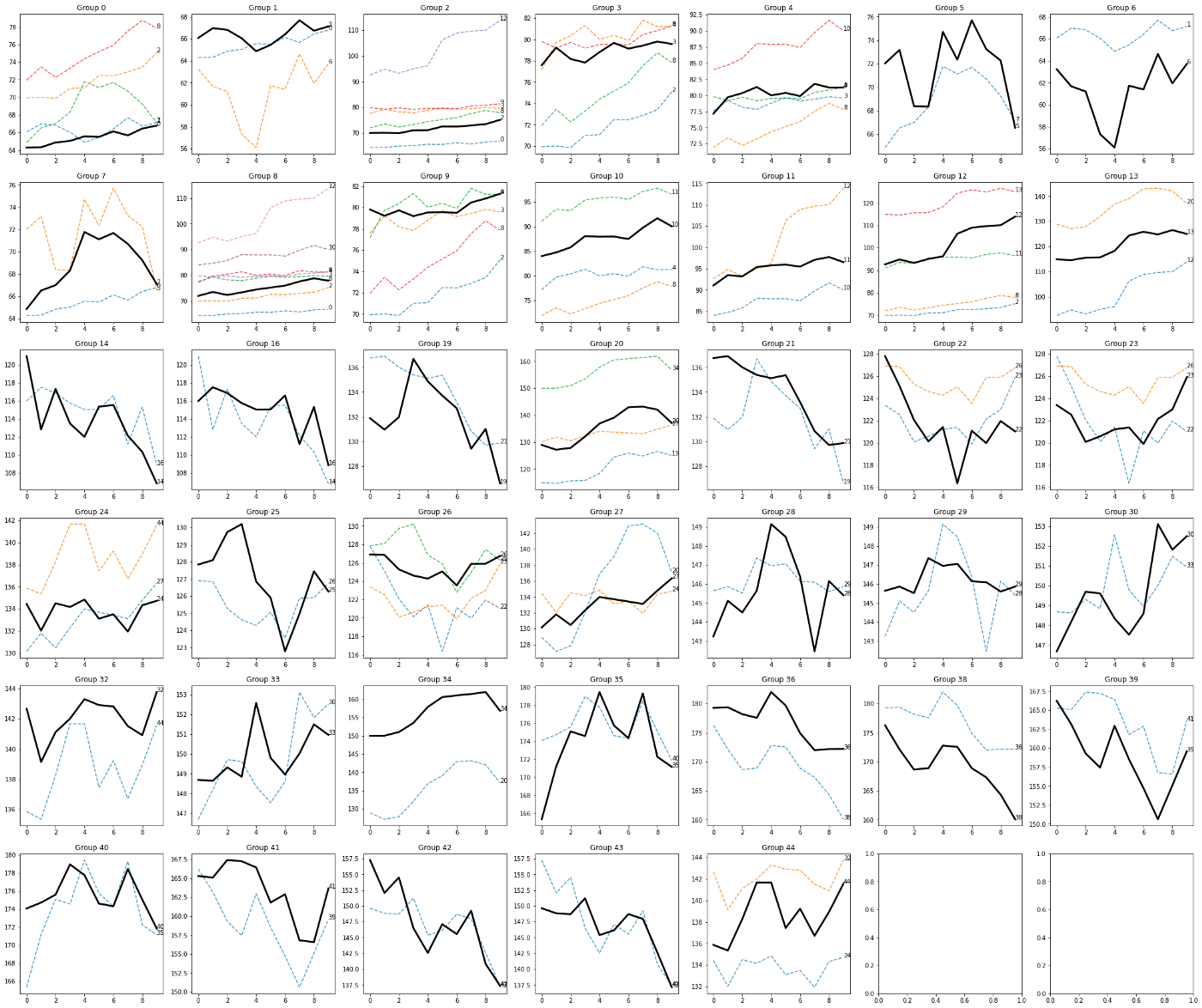
La logica sembra funzionare bene, poiché le linee nere, che sono le sequenze seme, sono circondate da sequenze simili sia in termini di anatomia che di direzione.
Controlliamo un'altra combinazione di parametri.
N = 25
K = 0.60
THRESHOLD = 25
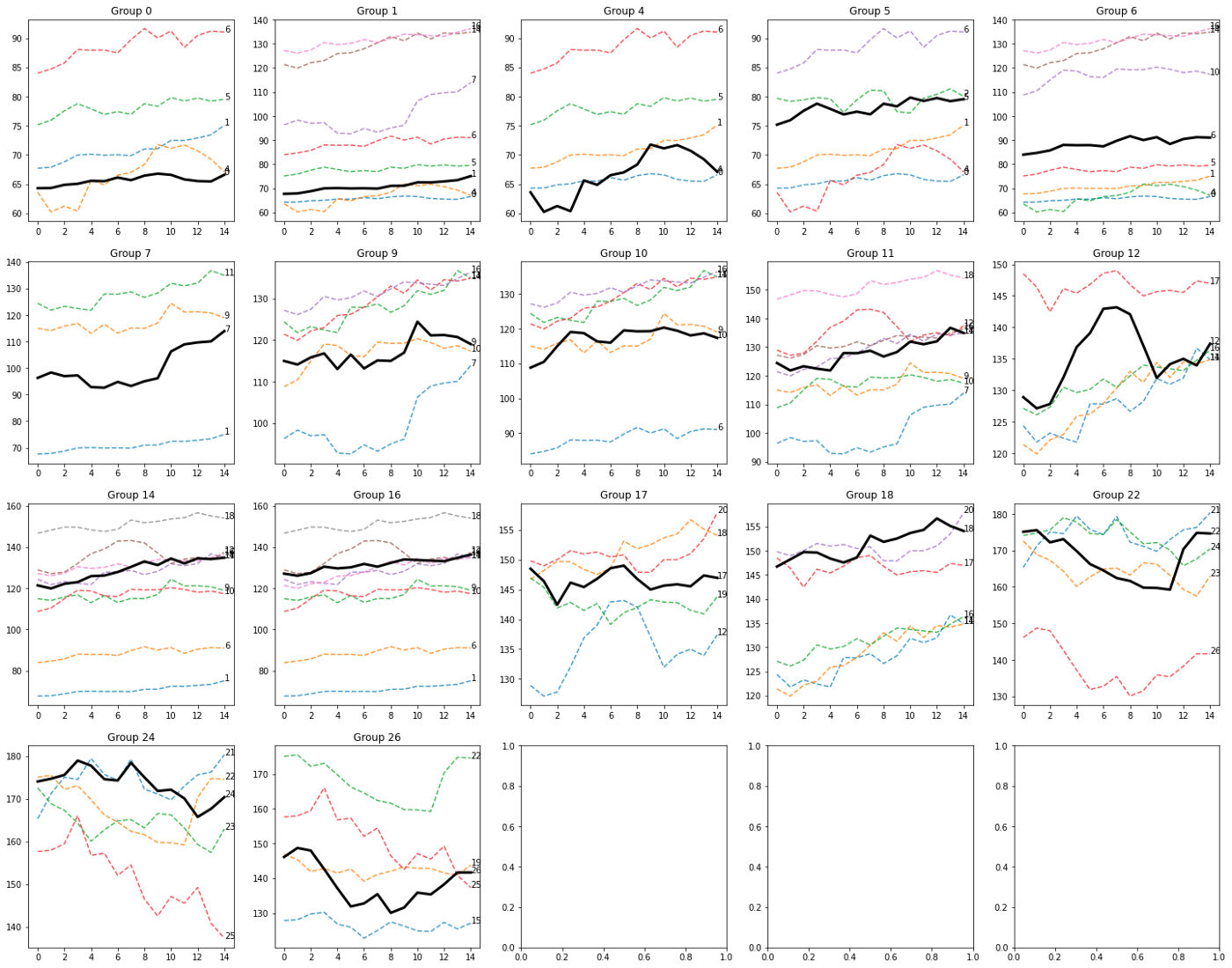
I risultati possono cambiare drasticamente in base ai parametri di input. Ciò è previsto poiché la dimensione della finestra, la dimensione della divisione della sequenza A/B e la soglia influiscono in maniera importante sulla logica dell'algoritmo di clustering.
Alcuni modelli spiccano davvero, come questo nel gruppo 22
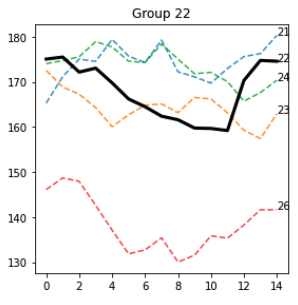
e gruppo 26
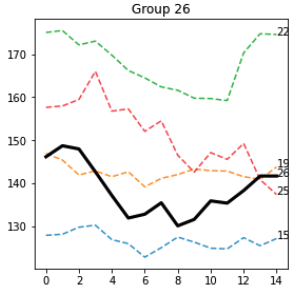
La maggior parte delle sequenze attorno alla sequenza seed sono effettivamente simili e condividono visivamente diverse caratteristiche. Credo che sia necessaria una metodologia più accurata per valutare queste proprietà.
Anche se sono sicuro che esiste un modo migliore per calcolare il punteggio, questi risultati mi sembrano promettenti!
Calcolare le probabilità
Ci avviciniamo all'ultima sezione di questo articolo. Ora calcoleremo la probabilità di avere un trend rialzista, ribassista o stabile per le sequenze B. Ricordiamo che B segue sempre A — il che significa che il primo elemento di \( B_i \) segue il rispettivo elemento di \( A_i \).
Definiremo un'altra funzione di supporto chiamata classify_trend che è responsabile del calcolo della pendenza e della comprensione della direzione generale della sequenza B.
def classify_trend(b, threshold=0.05):
"""
Classify the trend of a vector
"""
# compute slope
slope = np.mean(np.diff(b) / np.diff(np.arange(len(b))))
# if slope is positive, the trend is upward
if slope + (slope * threshold) > 0:
return 1
# if slope is negative, the trend is downward
elif slope - (slope * threshold) < 0:
return -1
# if slope is close to 0, the trend is flat
else:
return 0
# flatten list
flattened_G = [item for sublist in G.values() for item in sublist]
trends = [classify_trend(B[i]) for i in flattened_G]
# what is the probability of seeing a trend given the A sequence?
PROBABILITIES = {}
for k, v in G.items():
for seq in v:
total = len(v)
seq_trends = [classify_trend(B[seq]) for seq in v]
prob_up = len([t for t in seq_trends if t == 1]) / total
prob_down = len([t for t in seq_trends if t == -1]) / total
prob_stable = len([t for t in seq_trends if t == 0]) / total
PROBABILITIES[k] = {'up': prob_up, 'down': prob_down, 'stable': prob_stable}
# Let's pack all in a Pandas DataFrame for an easier use
probs_df = pd.DataFrame(PROBABILITIES).T
# create a column that contains the number of elements in the group
probs_df['n_elements'] = probs_df.apply(lambda row: len(G[row.name]), axis=1)
probs_df.sort_values(by=["n_elements"], ascending=False, inplace=True)e questi sono i risultati
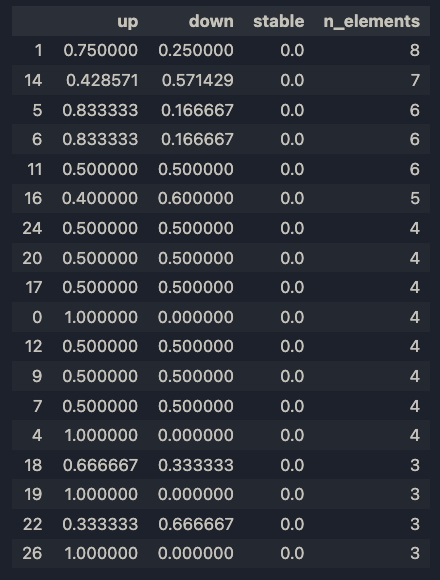
Visualizziamo le distribuzioni di probabilità.
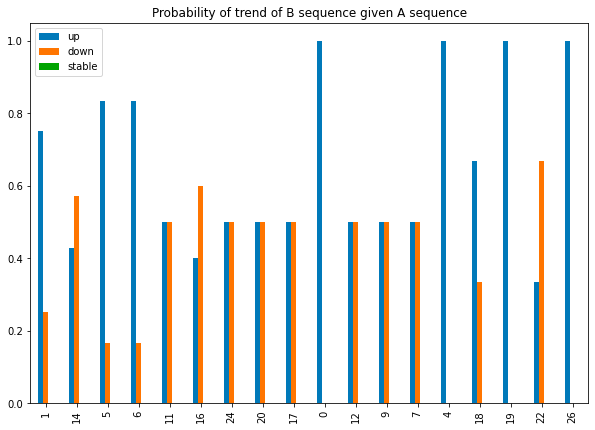
Ho scelto di ordinare gli elementi per n_elements, poiché più le sequenze sono raggruppate, più rilevante è il raggruppamento. In effetti, i gruppi 1 e 14 hanno rispettivamente 8 e 7 elementi, che sono molti modelli simili.
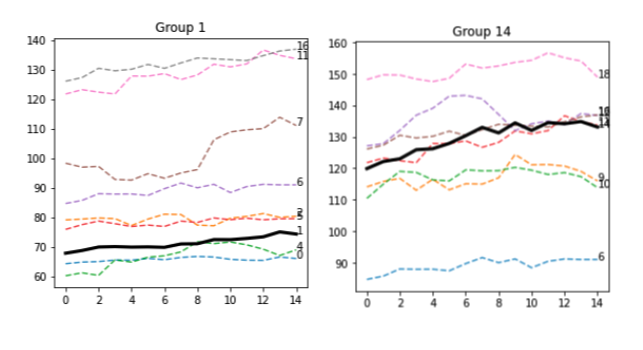
Questo non è sorprendente, poiché entrambe le sequenze A sono sostanzialmente piatte. C'è sicuramente spazio per l'ottimizzazione qui, come, ad esempio, la rimozione di tutte le linee piatte. Ma lo vedremo in futuro. In ogni caso, il 75% delle sequenze B nel Gruppo 1 ha una direzione verso l'alto, mentre il 57% delle sequenze B nel Gruppo 14 ha una direzione verso il basso. Forse le due linee sono davvero diverse per alcuni aspetti, o questo effetto è solo casuale - non possiamo dirlo al momento. Tracciamo le sequenze B.
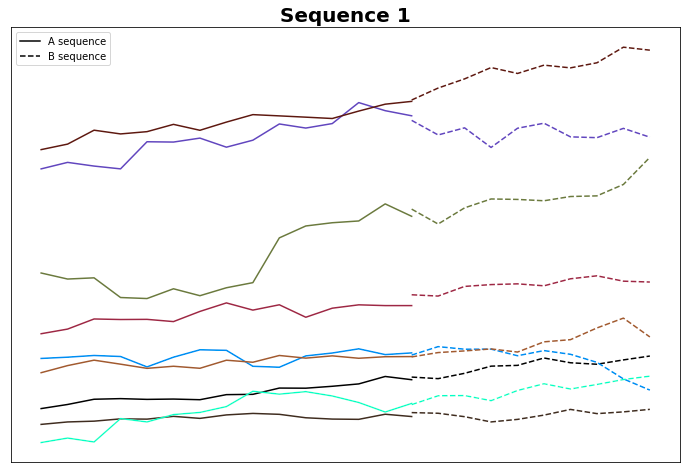
La maggior parte di queste sequenze B ha un trend effettivamente rialzista. C'è del lavoro da fare per garantire che questo non sia solo rumore.
Controlliamo il gruppo 14
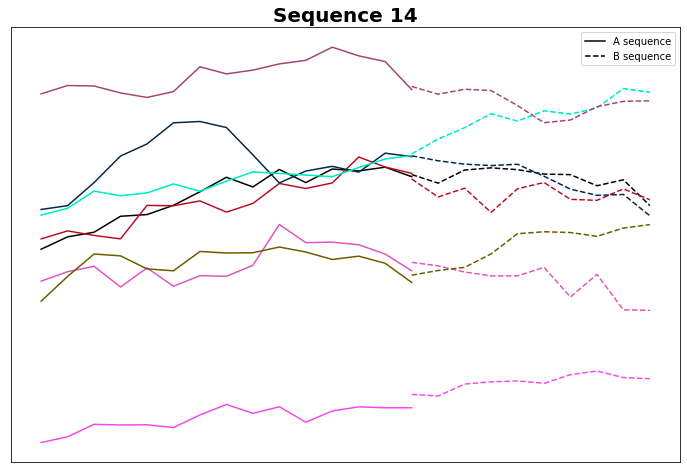
E in effetti, la maggior parte di loro ha un trend ribassista. Anche se la logica sembra essere corretta, forse il calcolo della pendenza ha bisogno di essere rivisito: forse possiamo aumentare la soglia dal valore predefinito 0,05... ma lo vedremo nel prossimo articolo.
Giusto per pura curiosità, tracciamo il Gruppo 22, che sembra interessante anche dal punto di vista visivo.
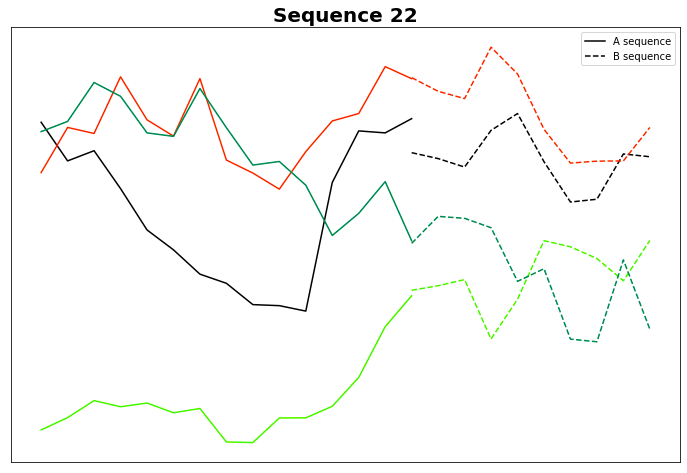
Sono solo io o le sequenze B sembrano davvero simili tra loro? Sebbene ciò richieda un'analisi approfondita, se ciò si rivela vero, allora A potrebbe davvero prevedere B e questo, di conseguenza, spiegherebbe perché vediamo B simili.
Conclusione della parte 1
In questa prima parte abbiamo visto come funziona l'algoritmo e il potenziale che potrebbe avere nel prevedere le tendenze del mercato azionario.
In realtà, se funziona, potrebbe essere potenzialmente un approccio generale...applicabile a qualsiasi serie temporale. Amplierò l'analisi nel prossimo futuro mentre continuo a lavorare sul progetto.
Condividi i tuoi commenti, dubbi e pensieri sul metodo. Mi piacerebbe integrare feedback e contributo! 😊







Commenti dalla community