Tabella dei Contenuti
Le reti neurali sono tra gli strumenti più potenti e affascinanti dell'intelligenza artificiale. Vengono spesso descritte come modelli "black-box" poiché il loro funzionamento interno è in parte misterioso, ma riescono comunque a ottenere risultati sorprendenti.
In questo articolo, esploreremo un passaggio chiave del loro processo di apprendimento ovvero l'algoritmo di backpropagation. Nello specifico vedremo come, grazie a tale tecnica, le reti neurali siano in grado di “apprendere” effettuando previsioni sempre più accurate.
- Cosa è l'algoritmo di backpropagation
- Concetti di forward pass, funzione di perdita, pesi e bias
- Come una rete neurale apprende pattern da dati supervisionati
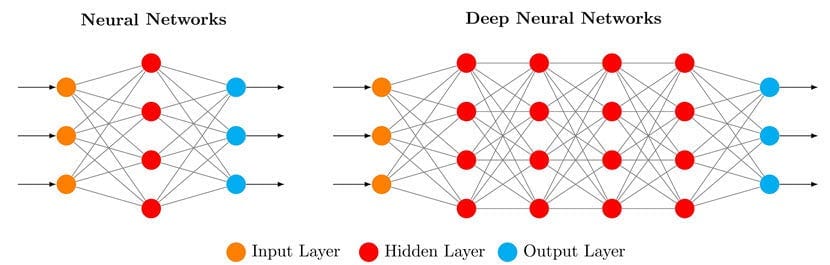
Una rete neurale è costituita da nodi (chiamati anche neuroni) e dalle connessioni che intercorrono tra tali nodi. In un’architettura tipica è possibile individuare un livello di input, uno di output e diversi livelli intermedi spesso noti come hidden layers (strati nascosti).
Ogni connessione tra nodi è caratterizzata da un peso il quale, durante l'addestramento, viene continuamente aggiornato. Il peso può essere visto come un moltiplicatore che aumenta o diminuisce il contributo di un nodo a quello nel livello successivo. Pertanto, il peso di una connessione stabilisce la quantità di input che viene trasmessa al nodo successivo, influenzando così il risultato finale della rete.
Sebbene un nodo riceva input da ciascun nodo del livello precedente, non tutti questi input hanno la stessa importanza. A ciascun nodo può anche essere assegnato un bias, ovvero un valore costante che viene aggiunto alla somma degli input ponderati provenienti dai neuroni del livello precedente.
Se vuoi leggere di più su pesi, bias e altre caratteristiche di una rete neurale, leggi questo articolo 👇

Breve introduzione alla backpropagation
La tecnica di backpropagation, è stata introdotta negli anni 60, ma la sua importanza nel contesto del deep learning è stata compresa solo successivamente.
Infatti, nel 1986 gli scienziati David Rumelhart, Geoffrey Hinton e Ronald Williams pubblicarono un influente lavoro intitolato Learning Representations by Back-Propagating Errors. Questo studio diede nuova vita al campo delle reti neurali, poiché dimostrava come la backpropagation potesse rendere efficiente l'addestramento di reti complesse.
Fino ad allora, uno dei problemi principali delle reti neurali era l'incapacità di apprendere in modo efficace a causa dell'enorme numero di parametri da regolare. Grazie alla backpropagation questa sfida è stata portata con successo a termine, diventando uno dei fondamenti dell'addestramento delle reti neurali.
La definizione di backpropagation
Il termine backpropagation indica un algoritmo matematico che oggi è strumento chiave nel meccanismo di apprendimento nei modelli di machine learning, nonché essenziale per l'ottimizzazione delle reti neurali.
Lo scopo della backpropagation è addestrare una rete neurale a fare previsioni migliori attraverso l'apprendimento supervisionato. Approfondendo ulteriormente, l'obiettivo della backpropagation è determinare come pesi e bias del modello debbano essere regolati per minimizzare l'errore, misurato tramite una funzione di perdita (loss function), cioè una funzione che ci informa quanto grande sia l'errore del modello in fase di previsione.
A livello matematico, la backpropagation mira a calcolare il gradiente della funzione di perdita rispetto a ciascuno dei singoli parametri della rete neurale. In termini più semplici, la backpropagation utilizza la regola della catena per calcolare la velocità con cui la perdita cambia in risposta a qualsiasi modifica di un peso (o bias) specifico nella rete.

L'ingrediente segreto: la funzione di attivazione
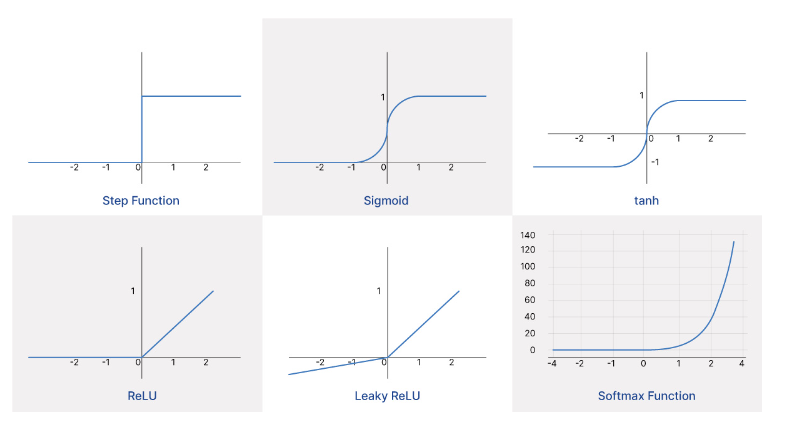
Le funzioni di attivazione introducono una forma di non linearità, permettendo così al modello di catturare schemi complessi nei dati di input e di generare gradienti. L'uso esclusivo di funzioni di attivazione lineari ridurrebbe essenzialmente la rete neurale a un modello di regressione lineare.
Le funzioni di attivazione comuni nelle reti neurali includono:
- La sigmoide, che mappa qualsiasi input a un valore tra 0 e 1.
- La tangente iperbolica (o tanh), che mappa gli input a un valore tra -1 e 1.
- La rectified linear unit (o ReLU), che mappa qualsiasi input negativo a 0 e lascia invariato qualsiasi input positivo.
- La softmax, che converte un vettore di input in un vettore i cui elementi variano tra 0 e 1 e la cui somma totale è 1.
Concetti Matematici per la Backpropagation
Derivate e differenziazione
La differenziazione è il processo matematico che ci permette di trovare la derivata di una funzione. In termini semplici, la derivata rappresenta il tasso di variazione di una funzione rispetto alla sua variabile indipendente. Se immaginiamo la funzione come una curva, la derivata in un punto specifico indica la pendenza della curva in quel punto. Questo è fondamentale nel contesto dell'apprendimento automatico, poiché la derivata ci aiuta a capire come cambiare i parametri di una funzione per ottimizzare un risultato.
Ad esempio, nella discesa del gradiente (un metodo di ottimizzazione usato per addestrare le reti neurali che vedremo a breve), utilizziamo la derivata per capire in che direzione muoverci per ridurre l'errore. Quando la derivata è positiva, significa che aumentando il valore dell'input aumenterà anche l'output. Al contrario, una derivata negativa indica che un aumento dell'input diminuirà l'output.
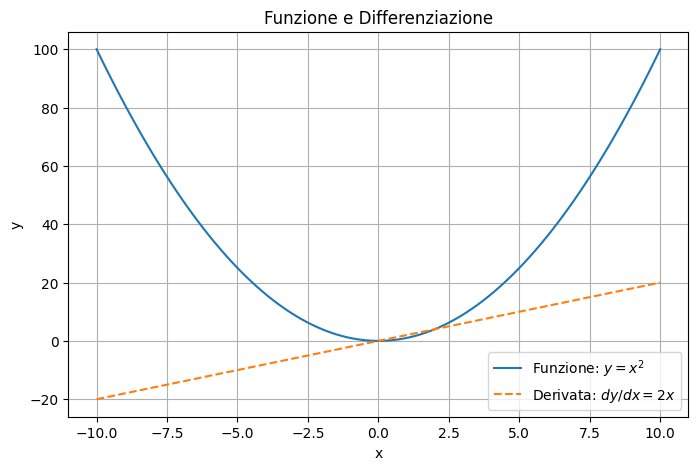
In questo grafico:
- La curva continua rappresenta la funzione \( y = x^2 \), una parabola
- La linea tratteggiata rappresenta la derivata della funzione \( \frac{dy}{dx} = 2x \) , che ci indica la pendenza della curva in ogni punto.
Quando la derivata è positiva (a destra dell'origine), la funzione è crescente, mentre a sinistra dell'origine (dove la derivata è negativa), la funzione è decrescente.
Machine Learning Engineering
Andriy Burkov
Questo è IL libro di IA applicata più completo in circolazione. È pieno di best practice e modelli di progettazione per la creazione di soluzioni di apprendimento automatico affidabili e scalabili.
Funzioni di attivazione
Le funzioni di attivazione dei singoli nodi in una rete neurale contengono molte variabili, inclusi i numerosi input provenienti dai neuroni dei livelli precedenti e i pesi applicati a tali input.
Quando analizziamo un nodo specifico, trovare le derivate parziali delle funzioni di attivazione dei neuroni del livello precedente ci consente di isolare l’impatto di ciascun input sull’output complessivo della funzione di attivazione.
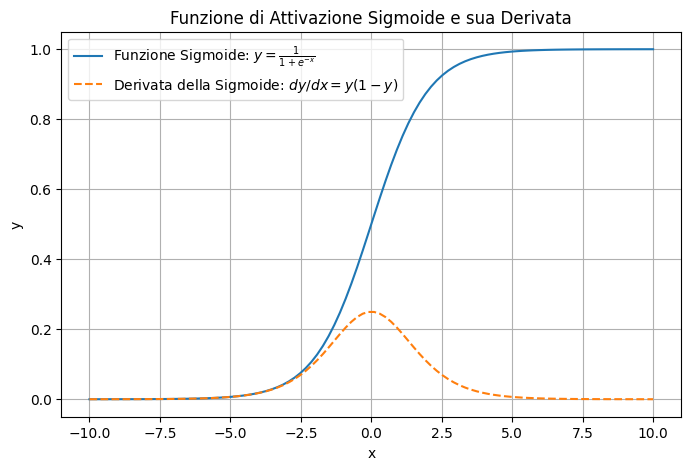
In questo grafico:
- La curva continua rappresenta la funzione di attivazione sigmoide, che trasforma i valori di input in un intervallo tra 0 e 1. La sigmoide è centrata attorno a \( x=0 \), dove passa per \( y=0.5 \)
- La linea tratteggiata rappresenta la derivata della sigmoide, che raggiunge il suo massimo intorno a \( x=0 \) e diminuisce rapidamente per valori di input lontani dallo zero.
In una rete neurale, ogni nodo (o neurone) riceve input da neuroni nei livelli precedenti, ognuno dei quali è moltiplicato per un peso che rappresenta l’importanza di quell’input per il nodo corrente. La funzione di attivazione quindi combina questi input ponderati e produce un output che viene passato al livello successivo. La presenza di molte variabili - gli input e i loro pesi - rende essenziale l’uso delle derivate parziali per analizzare come ogni singolo input influenzi l’output del nodo.
Le derivate parziali permettono di calcolare la variazione dell'output rispetto a una sola variabile alla volta, mantenendo costanti le altre. In pratica, calcolare le derivate parziali di una funzione di attivazione in relazione a ciascun input consente di valutare quanto ciascun input, con il suo peso associato, contribuisce al valore finale dell’output del neurone.
Questo processo è fondamentale per la backpropagation, in cui si aggiornano i pesi dei collegamenti in modo da ridurre l’errore complessivo della rete. La backpropagation si basa sull'idea che, per ridurre l’errore, è necessario calcolare esattamente quanto ciascun peso ha contribuito all’errore finale. Le derivate parziali aiutano a calcolare queste contribuzioni in modo preciso.
Concetto di gradiente
Un gradiente è un vettore che contiene tutte le derivate parziali di una funzione con più variabili. Rappresenta essenzialmente tutti i fattori che influenzano il tasso con cui l'output di un'equazione complessa cambia in seguito a una variazione dell'input.
La regola della catena (chain rule) è una formula per calcolare le derivate di funzioni che coinvolgono non solo più variabili, ma anche più funzioni. La regola viene usata convenientemente per calcolare le derivate delle funzioni di attivazione nelle reti neurali, che sono composte dagli output delle funzioni di attivazione di altri neuroni nei livelli precedenti.
Algoritmo di backpropagation
L'addestramento delle reti neurali tramite backpropagation comporta i seguenti passaggi:
- Propagazione in avanti (forward pass)
- Funzione di perdita (loss function)
- Retropropagazione dell'errore (backward pass)
- Discesa del gradiente (gradient descent)
La propagazione in avanti non è altro che una lunga serie di equazioni annidate, in cui gli output delle funzioni di attivazione di uno strato di nodi fungono da input per le funzioni di attivazione dei nodi nello strato successivo. L'addestramento del modello inizia tipicamente con un'inizializzazione casuale di pesi e bias.
In ogni "passaggio in avanti", un input viene campionato dal set di dati di addestramento. I nodi dello strato di input ricevono il vettore di input e ciascuno trasmette il proprio valore (moltiplicato per un peso iniziale casuale) ai nodi del primo strato nascosto. Le unità nascoste prendono la somma ponderata di questi valori di output come input per una funzione di attivazione, il cui valore di output (condizionato da un peso iniziale casuale) serve come input ai nodi nello strato successivo. Questo processo continua fino allo strato di output, dove avviene la previsione finale.
Dopo ogni passaggio in avanti, una funzione di perdita misura la differenza tra l'output previsto dal modello per un dato input e le previsioni corrette per quell'input. Dal punto di vista pratico, valuta in quale misura l'output effettivo del modello differisce dall'output desiderato.
Poiché la funzione di perdita prende l'output di una rete neurale come input e quell'output è una funzione complessa la quale comprende numerose funzioni di attivazione annidate dei singoli neuroni, la differenziazione della funzione di perdita comporta la differenziazione dell'intera rete. Pertanto, la backpropagation utilizza la regola della catena per fare ciò.
Partendo dallo strato finale della rete neurale, il "passaggio all'indietro" serve a calcolare come ogni parametro della rete contribuisca all'errore totale per un singolo input.
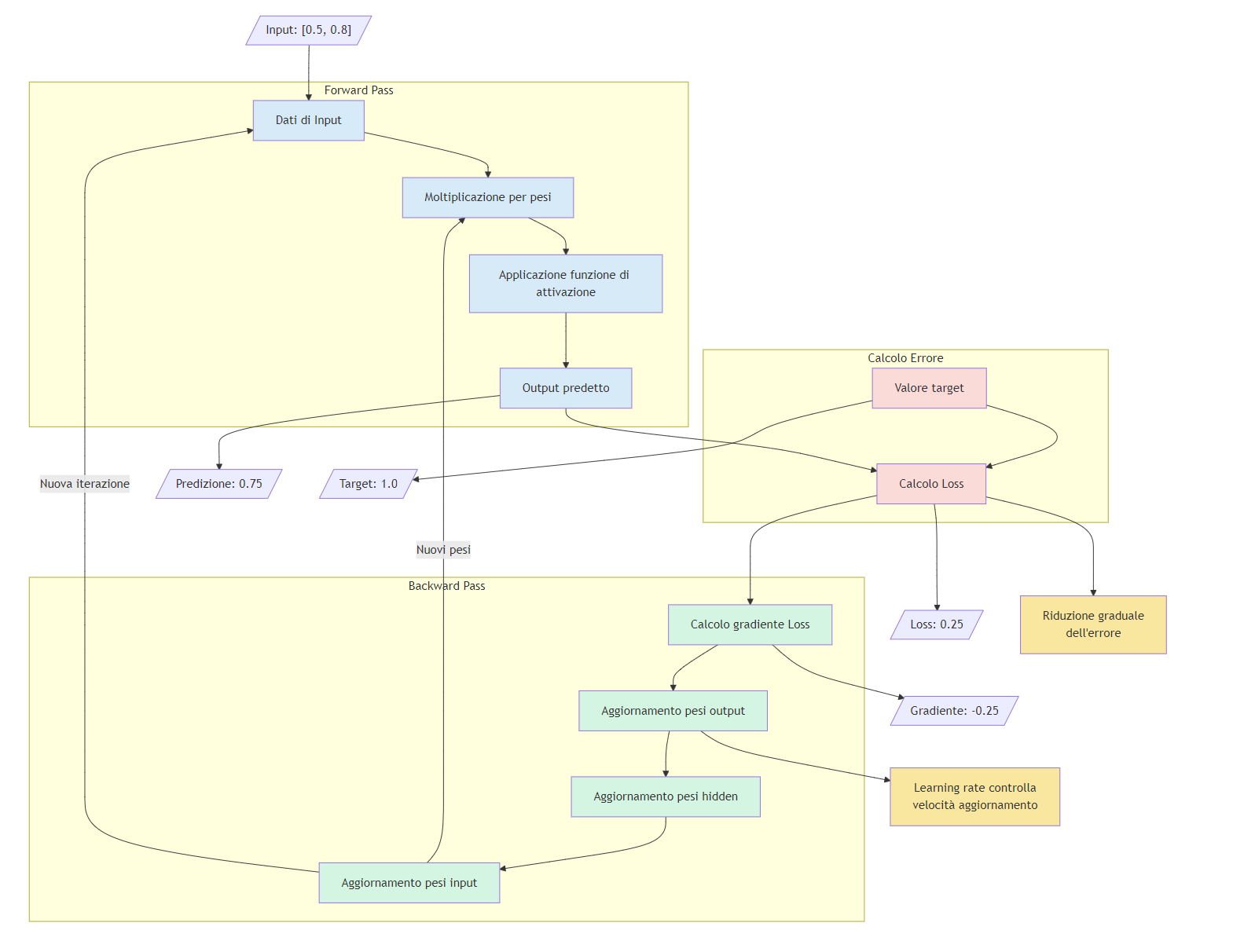
Alla fine, otteniamo il gradiente della funzione di perdita, che è un insieme di derivate parziali per ciascun peso e parametro di bias nella rete.
Abbiamo completato sia il passaggio in avanti che il passaggio all'indietro per un singolo esempio di addestramento.
Tuttavia, il nostro obiettivo è fare in modo che il modello generalizzi bene a nuovi input. Per raggiungere questo obiettivo, è necessario addestrarsi su un gran numero di campioni che riflettano la varietà e la gamma degli input su cui il modello dovrà fare previsioni una volta terminato l'addestramento.
Una volta ottenuti gradienti della funzione di perdita rispetto a ciascun peso e parametro di bias nella rete, possiamo minimizzare la funzione di perdita e quindi ottimizzare il modello utilizzando la discesa del gradiente per aggiornare i parametri del modello. Infatti, muovendosi lungo il gradiente della funzione di perdita, ridurremo così la perdita effettiva.
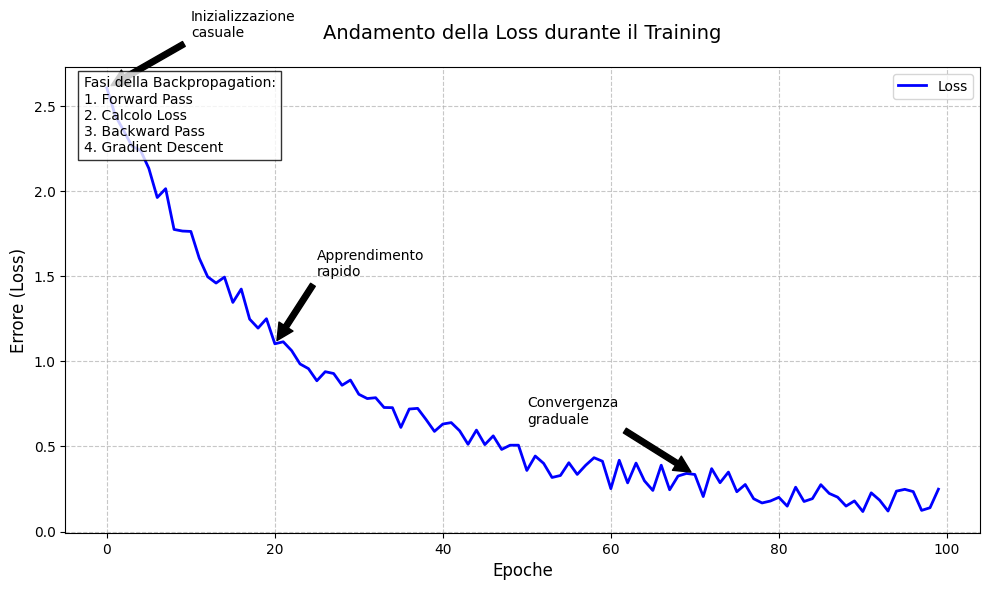
Poiché il gradiente che abbiamo calcolato durante il passaggio all'indietro contiene le derivate parziali per ogni parametro del modello, sappiamo in quale direzione passare ciascuno dei nostri parametri per ridurre la perdita. Ogni passaggio riflette come il modello “apprende” dai suoi dati di addestramento. Pertanto, il nostro obiettivo è quello di aggiornare iterativamente i pesi fino a raggiungere il gradiente minimo.
Conclusione
Hai imparato cosa è l'algoritmo di backpropagation e come questo sia fondamentale per l'apprendimento nelle reti neurali. Senza di essa, le reti neurali non sarebbero in grado di apprendere in modo efficace da grandi volumi di dati, né di sviluppare rappresentazioni complesse.
Nonostante il meccanismo di funzionamento interno della rete rimanga una "scatola nera", grazie alla backpropagation possiamo assicurarci che la rete impari, correggendo continuamente i suoi errori. Tale processo rappresenta una delle principali innovazioni che ha permesso all'intelligenza artificiale di evolversi fino alle applicazioni avanzate di oggi.









Commenti dalla community