Algoritmi e strutture dati per la data science in Python - Parte 1

Questo articolo ti guiderà attraverso i principali algoritmi e strutture dati usando Python puro come linguaggio di programmazione per la loro implementazione.

È lecito chiedersi perché conoscere questi algoritmi come persone che lavorano principalmente con i dati. Un data scientist non è diverso da uno sviluppatore a tutto tondo e la distinzione si nota nella sua specializzazione, cioè quella a lavorare con e trovare soluzioni basate sui dati.

Le risposte sono fondamentalmente due

Spesso e volentieri algoritmi e strutture dati sono progettate all'interno degli strumenti più comuni, anche nel linguaggio di programmazione stesso. Infatti, è estremamente raro per un programmatore oggi scrivere da zero algoritmi di ordinamento, perché quelli già implementati nelle librerie e linguaggi più comuni sono estremamente efficienti.

Tendenzialmente, gli algoritmi vanno conosciuti più che implementati praticamente in un progetto reale - essi forniscono metodi sistemici per risolvere una vasta gamma di problemi, inclusi quelli incontrati nell'analisi dei dati. La capacità di applicare alcuni di questi algoritmi a problemi specifici può aiutare i data scientist a sviluppare soluzioni efficaci e a vendersi meglio sul mercato.

Ad esempio, è spesso necessario cercare pattern o informazioni specifiche all'interno di grandi quantità di testo. Gli algoritmi di ricerca (i primi ad essere trattati in questo articolo) su testo sono essenziali per l'estrazione di informazioni significative da documenti, articoli, tweet e altro ancora.

Per ogni algoritmo avrai a disposizione una spiegazione di come funziona e la sua implementazione in Python che potrai usare a tuo piacimento.

In questa prima parte imparerai

• la notazione Big O per valutare la complessità di un algoritmo
• gli algoritmi di ricerca lineare e binaria
• gli algoritmi di ordinamento a bolle e coda
• la struttura dati della lista concatenata (linked list)

L'articolo sarà diviso in più parti per facilitare la lettura.

Iniziamo subito.

Notazione Big O - Quanto veloce è il nostro algoritmo?

Scrivere un algoritmo ci mette davanti subito ad una domanda: quanto veloce è a processare i miei dati?

Generalmente parlando, conviene quasi sempre scegliere l'algoritmo più veloce per risparmiare tempo e risorse computazionali.

La notazione Big O ci aiuta a capire quanto veloce è un algoritmo.

Big O ci aiuta a categorizzare i requisiti temporali o di memoria di algoritmo basandosi sul suo input. Non è fatto per fornire delle indicazioni puntuali su questi requisiti, piuttosto per darci una idea di quanto cresca la complessità del nostro algoritmo in base al suo input.

Usare Big O ci aiuta a prendere decisioni su quali algoritmi o strutture dati da usare. Sapere come performeranno ci può aiutare molto nello scrivere del software performante.

Facciamo un esempio pratico di come categorizzare una semplice funzione.

def sum_char_codes(string: str) -> int:
    sum = 0
    for char in string:
        sum += ord(char)
    return sum

result = sum_char_codes("Hello")
print(result)  
>>> 532

La funzione sum_char_codes accetta una stringa come input e restituisce la somma dei punti di codice unicode (valori interi che rappresentano i caratteri) di tutti i caratteri nella stringa.

In altre parole, scorre ogni carattere nella stringa di input, trova l'unicode per quel carattere utilizzando la funzione ord e lo aggiunge a una somma parziale. Infine, restituisce la somma totale di tutti i punti del codice carattere.

La domanda alla quale risponde Big O è: all'aumentare del nostro input, quanto aumenta la spesa computazionale del nostro algoritmo?

In questa funzione, stiamo di fatto trattando la stringa in input come una lista che contiene dei valori, i caratteri che la compongono. Significa che per poter sommare gli elementi, dobbiamo considerare sempre ogni carattere della stringa.

Significa che se il numero di caratteri nella nostra stringa aumenta del 50%, allora la funzione dovrà considerare il 50% in più di caratteri da processare. Per ogni carattere aggiuntivo nella stringa, c'è un ciclo in più che lo deve considerare.

La crescita si dice lineare, ed denotata dal simbolo O(n), poiché n è il numero di elementi che compongono la stringa e quelli sottoposti alla logica dell'algoritmo.

Consideriamo ora la stessa funzione di prima, ma con una piccola aggiunta

def sum_char_codes(string: str) -> int:
    sum = 0
    for char in string:
        sum += ord(char)
    for char in string:
        sum += ord(char)
    return sum

Ho aumentato il numero di cicli a scopo dimostrativo. Qual è la sua complessità Big O ora? Prenditi un minuto per rispondere.

Se hai detto O(2n) posso dirti che sei sulla strada giusta, ma non è corretto!

Infatti, nella notazione Big O le costanti vengono sempre omesse. Questo perché l'obiettivo della notazione Big O non è quella di darti delle indicazioni precise su quanto complesso diventa il tuo algoritmo, quanto darti una idea della sua complessità generale. La costante è spesso irrilevante!

Prendi questo per esempio:

Poniamo n = 1, O(10n) = 10, O(n^2) = 1

Ora poniamo n=5, O(10n) = 50, O(n^2) = 25

Infine poniamo n=100, O(100n) = 1000, O(n^2) = 10000

Semplicemente andando da 1 a 100 elementi in input, la complessità aumenta di 10x se consideriamo la sua elevazione al quadrato. È importante considerare le costanti, ma ai fini di comprendere quanto veloce è il nostro algoritmo, ci basta identificare come n i casi in cui la ricerca risulti lineare.

Facciamo un altro esempio con una ulteriore modifica alla funzione

def sum_char_codes(string: str) -> int:
    sum = 0
    for char in string:
        symbol = ord(char)
        if symbol == 69:
          return sum
        sum += symbol
    return sum

In questo caso ho inserito una condizione che restituisce la somma non appena la conversione numerica del carattere sia uguale a 69. Qual è la complessità Big O di questa nuova versione? Prenditi un minuto per rispondere.

È sempre O(n)! Questo perché Big O tende a considerare sempre il peggiore dei casi (worst case scenario). In questo caso potremmo dire che nel peggiore dei casi, io dovrò sempre cercare tra tutti gli elementi della lista, cioè n.

Vediamo ancora un altro esempio, dove si aumenta la complessità

def sum_char_codes(string: str) -> int:
    sum = 0
    for char in string:
      for char in string:
        symbol = ord(char)
        sum += symbol
    return sum

Un doppio ciclo, uno dentro l'altro. Rileggi il trucchetto di prima - qual è la sua complessità ora?

O(n^2). Questo perché per ogni elemento della lista, applico un nuovo ciclo.

In basso una chiara rappresentazione delle varie complessità Big O e di come queste cambiano in relazione al numero di elementi in input.

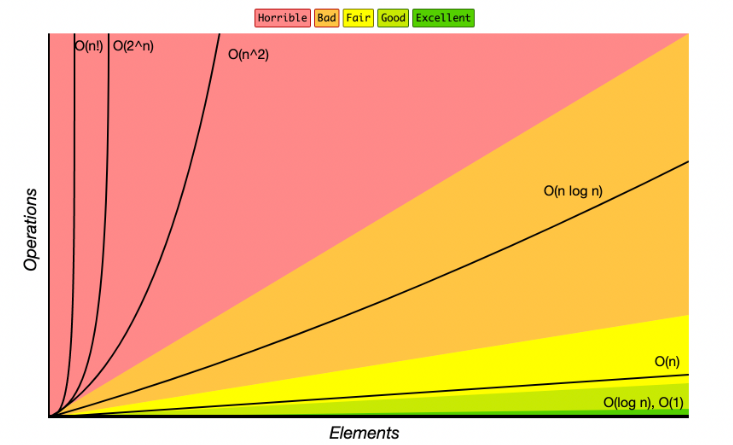
Ricapitolando:

• Big O indica la crescita di complessità di un algoritmo rispetto al suo input
• Le costanti sono omesse
• Si misura tipicamente il worst case scenario

Ricordare questi tre punti ti aiuterà a poter valutare efficacemente gli algoritmi che hai davanti.

Ricerca

Gli algoritmi di ricerca servono per trovare uno o più elementi all'interno di un insieme più ampio di elementi. Questi algoritmi sono ampiamente utilizzati in informatica e sono fondamentali per molte applicazioni, inclusi i motori di ricerca su Internet.

Nella data science, si usano molto spesso in compiti di data mining e di intelligence.

Algoritmo: Ricerca lineare

La ricerca lineare rappresenta sicuramente l'algoritmo di ricerca più semplice e sicuramente la base per algoritmi di ricerca più complessi.

La ricerca lineare controlla ogni elemento della lista per identificare l'elemento target. La sua complessità temporale è dunque O(n) poiché cresce linearmente con la crescita della lista in input.

Definiamo la funzione di ricerca lineare in questo modo:

def linear_search(arr: list[int], target_value: int):
  for index, item in enumerate(arr): # iterare per ogni elemento dell'array
    if item == target_value: # se l'elemento corrisponde, restituisci l'elemento oppure la sua posizione
      return index
  return -1 # se non trova l'item target, allora comunicalo con -1

a = [0, 1, 2, 3, 4, 69, 42]
linear_search(arr=a, target_value=69)
>>> 5

Va specificato che la lista e il valore da ricercare devono essere dello stesso tipo (non è possibile avere una lista di numeri interi e cercare una stringa). Un algoritmo semplice e facilmente implementabile anche da uno sviluppatore alle prime armi.

Algoritmo: Ricerca binaria

L'algoritmo di ricerca binaria è solitamente il primo algoritmo di ricerca che si studia, tralasciando quello di ricerca lineare, su cui si basa.

La ricerca binaria funziona dividendo ripetutamente l'intervallo di ricerca a metà. In una metà ci sarà il nostro valore target, nell'altra no. Per questo viene chiamata ricerca "binaria" (0, 1).

Questi sono gli step dell'algoritmo:

1. Si inizia con una lista ordinata di elementi
2. Si settano due puntatori, low e high, che puntano rispettivamente al primo e all'ultimo elemento della lista
3. Si calcola la media tra low e highun valore chiamato mid
4. Si confronta l'elemento a mid con il valore target:
   1. Se mid == target, allora si restituisce l'indice di mid
   2. Se mid > target, allora il target deve trovarsi nella metà sinistra, quindi si aggiorna high = mid - 1
   3. Se mid < target, allora il target deve trovarsi nella metà destra, quindi si aggiorna low = mid + 1
5. Si ripetono i passaggi 3 e 4 finché non viene trovato il target o finché low non diventa maggiore di high (il che significa che il valore di destinazione non è presente nell'array).

Il vantaggio principale della ricerca binaria è la complessità temporale O(log n), che è molto migliore della complessità temporale O(n) dell'algoritmo di ricerca lineare, soprattutto per array di grandi dimensioni.

Perché O(log n)? Perché sono necessari log n step per arrivare al singolo valore target.

Immaginiamo di avere una lista di 4096 valori. Applicando l'algoritmo di ricerca binaria avremo

(inizio) 4096
1. 2048
2. 1024
3. 512
4. 256
5. 128
6. 64
7. 32
8. 16
9. 8
10. 4
11. 2
12. 1 (fine)

12 step, proprio perché log 4096 = 12. Nel caso peggiore, dovremmo fare 12 iterazioni dell'algoritmo di ricerca binaria per trovare l'elemento.

Facciamo un altro esempio.

Indovina il numero alla quale io sto pensando. Questo è compreso tra 0 e 100. Qual è il modo migliore per indovinare questo numero?

Ragioniamo un attimo: se dovessi usare una ricerca lineare dovrei proporre possibilmente ogni numero da 0 a 100 per trovare il numero target. La sua complessità temporale sarebbe proprio 100 (n). Usiamo la ricerca binaria invece!

Iniziamo con 50. Troppo basso!
75. Troppo alto!
63. Troppo alto!
57. Risposta esatta!

Abbiamo sostanzialmente eliminato 100 step per averne al massimo 7:

100 possibili numeri -> 50 -> 25 -> 13 -> 7 -> 4 -> 2 -> 1.

Quindi, log n.

La ricerca binaria funziona solo su liste ordinate.

def binary_search(sorted_list: list[int], item: int) -> int:
    lo = 0
    hi = len(sorted_list)
    while low <= high:
        m = lo + (hi - lo) // 2
        current_item = sorted_list[mid]
        if current_item == item:
            return m
        elif item < current_item:
            hi = m
        else:
            lo = m + 1
    return -1

Ecco una rappresentazione grafica che mette a confronto al ricerca binaria e quella lineare.

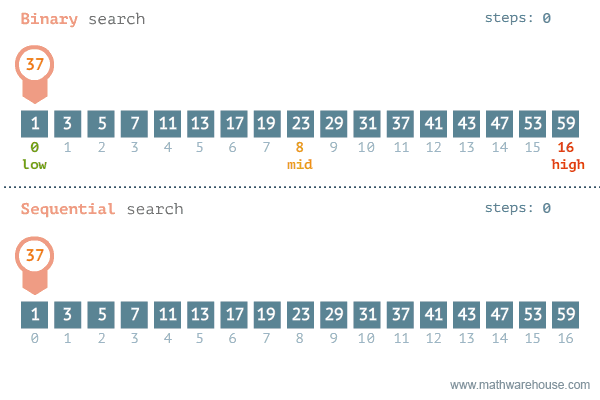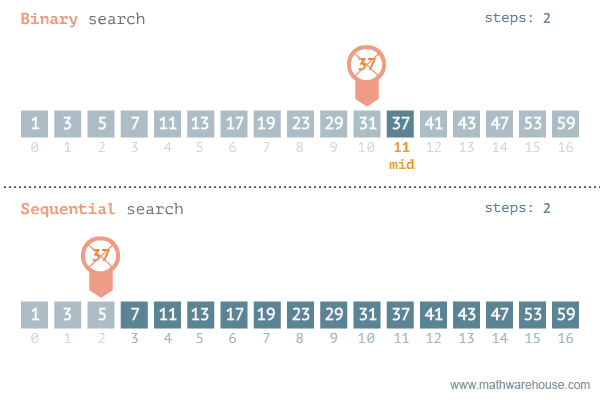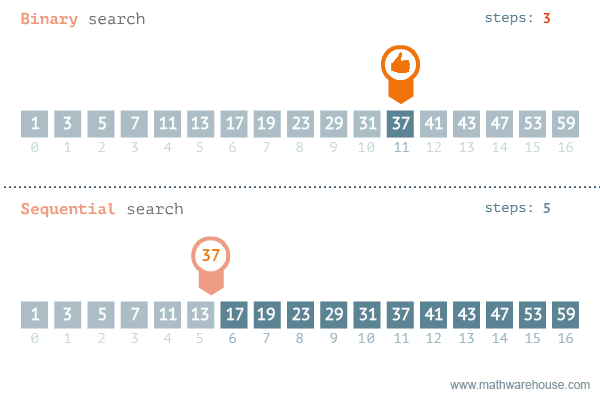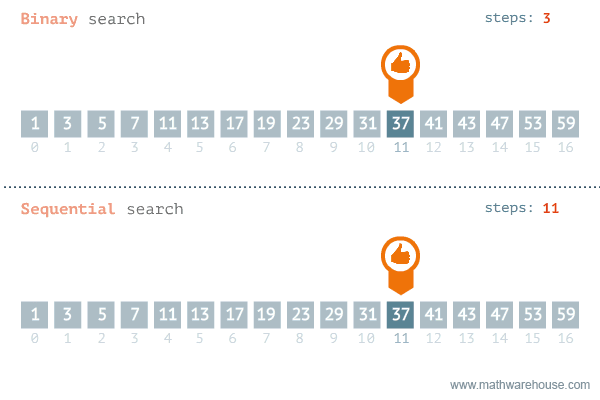
Nella data science, la ricerca binaria può essere utilizzata come elemento costitutivo per algoritmi più complessi utilizzati nell'apprendimento automatico, come algoritmi per l'addestramento di reti neurali o per trovare gli iperparametri ottimali per un modello.

Ordinamento

Implementeremo due algoritmi di ordinamento, bubble sort (ordinamento a bolle) e queue (coda) passando per la struttura dati conosciuta come lista concatenata (linked list in inglese).

Bubble sort è un algoritmo semplice da capire, ma il suo valore educazionale è alto: la sua semplicità lo rende un algoritmo cruciale da studiare e comprendere . Serve come trampolino di lancio per l'apprendimento di algoritmi più complessi e contribuisce alla comprensione generale e al progresso delle tecniche di ordinamento.

Una coda invece è una declinazione della lista concatenata, una struttura dati molto importante. Una lista concatenata è una struttura di dati lineare in cui gli elementi non sono archiviati in posizioni di memoria contigue come nelle liste. Invece, ogni elemento in un elenco collegato è un oggetto separato che contiene dati e un riferimento (o puntatore) all'elemento successivo nella sequenza.

Algoritmo: Bubble sort (ordinamento a bolle)

Uno degli algoritmi più semplici e fondamentali nell'ambito dell'ordinamento di liste.

La logica di bubble sort è estremamente semplice: scorre ripetutamente l'elenco di input, confronta gli elementi adiacenti e li scambia se sono nell'ordine sbagliato. Il passaggio attraverso l'elenco viene ripetuto finché l'elenco non viene ordinato.

Fine. 😄

L'algoritmo bubble sort si può spiegare in questo modo:

1. Confronta i primi due elementi dell'elenco
2. Se il primo elemento è maggiore del secondo, allora questi vengono scambiati di posizione
3. Passa alla coppia di elementi successiva
4. Ripeti i passaggi 1-3 fino a raggiungere la fine della lista

Al completamento di una iterazione, l'elemento più grande "salirà a galla (come una bolla)" in ultima posizione nella lista.

Sebbene il bubble sort sia facile da comprendere e implementare, non è un algoritmo efficiente per liste di grandi dimensioni poiché la sua complessità temporale media nel caso peggiore è O(n^2).

Ecco un esempio pratico 👇

Poniamo di avere un array a = [1, 3, 7, 4, 2] e di volerlo ordinare dal numero più piccolo al più grande.

Applicando bubble sort guarderemo a ogni coppia di numeri

(1, 3): 3 è più grande di 1? Si. Nessuna azione.
(3, 7): 7 è più grande di 3? Si. Nessuna azione.
(7, 4): 7 è più grande di 4? No. I numeri vengono scambiati!
(7, 2): 7 è più grande di 2? No. I numeri vengono scambiati!
Fine della prima iterazione.

L'array alla fine della prima iterazione appare così, con il 7, il numero più grande, proprio alla fine.

a = [1, 3, 4, 2, 7]

Il codice Python per scrivere bubble sort è il seguente:

def bubble_sort(arr: list[int | float]) -> list[int | float]:
    for i in range(len(arr)):
        for j in range(len(arr) - 1 - i):
            if arr[j] > arr[j + 1]:
                tmp = arr[j]
                arr[j] = arr[j + 1]
                arr[j + 1] = tmp

Da notare che Bubble sort è un algoritmo distruttivo, cioè cambia l'input in modo irreversibile. È consigliato creare una copia dell'array prima di applicare bubble sort se si vuole evitare perdita di dati.

Essendo un algoritmo semplice per l'ordinamento, bubble sort non ha applicazioni oggi particolarmente utili. L'importanza di questo algoritmo è che costituisce la base degli algoritmi di ordinamento e permette di sbloccare capacità di problem solving nel programmatore.

Struttura Dati: Linked list (lista concatenata)

Una lista concatenata è una struttura dati costituita da una sequenza di nodi, ciascuno dei quali contiene:

1. Dati: il valore effettivo o le informazioni archiviate nel nodo.
2. Puntatore (o riferimento): un indirizzo di memoria che punta al nodo successivo nella sequenza.

In altre parole, una lista concatenata è una raccolta di nodi, dove ogni nodo possiede informazioni specifiche e un riferimento al nodo successivo nella lista, a cui punta.

Ciò consente a questa struttura dati di essere dinamica, il che significa che è possibile aggiungere o rimuovere nodi secondo necessità senza doversi preoccupare dell'allocazione di memoria contigua come faresti con un array.

Ecco alcune caratteristiche chiave delle liste collegate:

• Allocazione di memoria non contigua: i nodi vengono archiviati in posizioni di memoria non adiacenti
• Dimensione dinamica: gli elenchi collegati possono crescere o ridursi dinamicamente aggiungendo o rimuovendo nodi
• Nessuna capacità fissa: a differenza degli array, le linked list non hanno una dimensione massima predeterminata
• Accesso casuale: puoi scorrere l'elenco in qualsiasi direzione (avanti o indietro) utilizzando i puntatori

Gli elenchi concatenati sono comunemente utilizzati in informatica per varie applicazioni, come ad esempio:

• Implementazione di strutture dati come code (che vedremo a breve), stack e grafici
• Gestione dell'allocazione e deallocazione dinamica della memoria
• Fornire operazioni efficienti di inserimento, cancellazione e ricerca

Esistono diversi tipi di elenchi collegati, tra cui:

1. Lista concatenata singolarmente: ogni nodo ha solo un riferimento al nodo successivo
2. Lista doppiamente concatenata: ogni nodo ha riferimenti sia al nodo precedente che a quello successivo
3. Lista circolarmente concatenata: l'ultimo nodo punta al primo nodo, formando un cerchio

Nella data science, le liste concatenate sono concettualmente accumunate ai grafici di rete. Entrambi sono costituiti da nodi, che possono essere pensati come entità individuali (ad esempio persone, prodotti o concetti) e i loro collegamenti rappresentano le relazioni tra i nodi.

Sia le liste concatenate che i grafici di rete consentono di attraversare ed esplorare la struttura, che è essenziale per varie applicazioni (ad esempio, trovare i percorsi più brevi, identificare cluster o rilevare comunità). Nel contesto NLP possono essere dunque utilizzate per rappresentare l'albero di analisi di una frase o di un documento. Ogni nodo rappresenta una parola, una frase o un predicato e i collegamenti rappresentano le relazioni tra di loro.

In Python, una semplice lista concatenata singolarmente si scrive così

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None

class LinkedList:
    def __init__(self):
        self.head = None

    def append(self, data):
        new_node = Node(data)
        if not self.head:
            self.head = new_node
            return
        last_node = self.head
        while last_node.next:
            last_node = last_node.next
        last_node.next = new_node

    def prepend(self, data):
        new_node = Node(data)
        new_node.next = self.head
        self.head = new_node

    def delete(self, data):
        current_node = self.head
        if current_node and current_node.data == data:
            self.head = current_node.next
            current_node = None
            return
        previous_node = None
        while current_node and current_node.data != data:
            previous_node = current_node
            current_node = current_node.next
        if current_node is None:
            return
        previous_node.next = current_node.next
        current_node = None

    def print_list(self):
        current_node = self.head
        while current_node:
            print(current_node.data, end=" -> ")
            current_node = current_node.next
        print("None")


# Creazione 
ll = LinkedList()

ll.append(1)
ll.append(2)
ll.append(3)

# inserimento di un elemento
ll.prepend(0)

ll.print_list()

# rimozione di un elemento
ll.delete(2)
ll.print_list()

L'output di questo script è il seguente

>>> 0 -> 1 -> 2 -> 3 -> None
>>> 0 -> 1 -> 3 -> None

Struttura Dati: Coda (queue)

Una coda è una struttura dati fondamentale in informatica che segue il principio First-In-First-Out (FIFO).

È una raccolta lineare di elementi, dove gli elementi vengono aggiunti alla fine, nella parte posteriore (rear-end) della coda mentre l'elemento più vecchio (quello aggiunto per primo) viene rimosso dalla parte anteriore (front-end) della coda.

Ciò significa che una coda segue queste regole:

• Inserimento: i nuovi elementi vengono aggiunti alla fine della coda, spesso definita "accodamento" (o enqueuing) operazione
• Eliminazione: l'elemento più vecchio viene rimosso dalla coda, operazione spesso definita come l'operazione di "deaccodamento" (o dequeuing)

Ecco alcune caratteristiche chiave delle code:

• First-In-First-Out (FIFO): gli elementi vengono elaborati nell'ordine in cui sono stati aggiunti
• Last-In-Last-Out: l'elemento aggiunto più recentemente verrà rimosso per ultimo
• Conservazione dell'ordine: l'ordine originale degli elementi viene preservato man mano che gli elementi vengono inseriti ed eliminati

Utilizzando il codice della lista concatenata visto prima, possiamo creare una coda in Python così

class Queue:
    def __init__(self):
        self.items = LinkedList()

    def enqueue(self, data):
        self.items.append(data)

    def dequeue(self):
        if self.is_empty():
            return None
        else:
            data = self.items.head.data
            self.items.delete(data)
            return data

    def is_empty(self):
        return self.items.head is None

    def print_queue(self):
        self.items.print_list()

# Example usage:
queue = Queue()
queue.enqueue(1)
queue.enqueue(2)
queue.enqueue(3)
queue.enqueue(4)
queue.print_queue()  # Output: 1 -> 2 -> 3 -> 4 -> None
queue.dequeue()
queue.print_queue()  # Output: 2 -> 3 -> 4 -> None

Le code trovano particolare utilizzo nella data engineering. Le code possono essere utilizzate per gestire attività di elaborazione batch e nella pianificazione delle attività (job scheduling), per garantire che siano eseguiti in modo efficiente.

Operativamente parlando, un data scientist potrebbe creare una coda per creare e organizzare una pipeline di processing dei dati.

Un esempio qui che simula gli step di preprocessing di valori numerici e categoriali per un task di regressione.

def preprocess_numerical_data(data):
    # implementare le logiche per gestire le variabili numeriche, quali standardizzazione e altre trasformazioni
    pass

def preprocess_categorical_data(data):
    # implementare le logiche per gestire le variabili categoriali, quali one-hot encoding e altre trasformazioni
    pass

# Coda generale per la gestione del preprocessing
def preprocess_dataset(dataset):
    queue = Queue()
    # esempio non reale di come usare logiche di processing del dato in una coda
    for data in dataset:
        if isinstance(data, int) or isinstance(data, float):
            preprocessed_data = preprocess_numerical_data(data)
        else:
            preprocessed_data = preprocess_categorical_data(data)
        queue.enqueue(preprocessed_data)
    return queue

# Esempio
dataset = [10, 15.5, 'category_A', 'category_B', 20, 'category_C']

preprocessed_queue = preprocess_dataset(dataset)

while not preprocessed_queue.is_empty():
    print(preprocessed_queue.dequeue())

Conclusioni

Questo articolo rappresenta la prima parte di una serie più ampia di pezzi dedicati agli algoritmi e strutture dati importanti per data scientist e non.

Hai imparato alcuni algoritmi di base, come la ricerca lineare, binaria e il bubble sort, che sono molto semplici ma che rappresentano le mattonelle essenziali per costruire algoritmi più complessi.

È raro che userai questi algoritmi nella vita reale, ma in un contesto di selezione ti verranno probabilmente chiesti sia in linea teorica che pratica.

Tra gli argomenti trattati, quelli della lista concatenata e della coda sono sicuramente i più pratici e difficili sia da capire che da implementare. Si possono trovare moltissimi casi d'uso nella data science e machine learning che andrebbero a far uso di queste due strutture dati. Ti consiglio di studiarle per bene per capire le ripercussioni di tali strutture nel tuo software e di comprendere come strumenti come Airflow funzionano dietro alle quinte.

Il prossimo pezzo della serie verrà inserito qui non appena pubblicato.